题目内容
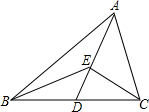 (1)如图所示,点D在△ABC的边BC上,连接AD,在线段AD上任取一点E.求证:∠BEC=∠ABE+∠ACE+∠BAC.
(1)如图所示,点D在△ABC的边BC上,连接AD,在线段AD上任取一点E.求证:∠BEC=∠ABE+∠ACE+∠BAC.(2)已知D在△ABC的边BC上,点E是线段AD所在直线上的任意一点,其中点E与点A、D不重合,且点E在△ABC外,连接BE、CE.请画出满足上述条件的图形,并写出∠BEC、∠ABE、∠ACE、∠BAC之间的关系.
考点:三角形的外角性质,三角形内角和定理
专题:
分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,再根据∠BAD+∠CAD=∠BAC证明;
(2)分点E在BC的下方时,利用四边形的内角和定理解答;点B在BC的上方时,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAD=∠ABE+∠AEB,∠CAD=∠ACE+∠AEC,再根据∠AEB+∠AEC=∠BEC解答.
(2)分点E在BC的下方时,利用四边形的内角和定理解答;点B在BC的上方时,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAD=∠ABE+∠AEB,∠CAD=∠ACE+∠AEC,再根据∠AEB+∠AEC=∠BEC解答.
解答: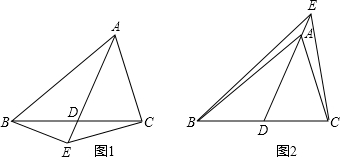 (1)证明:由三角形的外角性质得,∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,
(1)证明:由三角形的外角性质得,∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,
∵∠BAD+∠CAD=∠BAC,
∴∠BEC=∠BED+∠CED=∠ABE+∠BAD+∠ACE+∠CAD=∠ABE+∠ACE+∠BAC,
即:∠BEC=∠ABE+∠ACE+∠BAC;
(2)解:如图1,点E在BC的下方时,
由四边形的内角和定理得,∠BEC+∠ABE+∠ACE+∠BAC=360°;
如图2,点B在BC的上方时,
由三角形的内角和定理得,∠BAD=∠ABE+∠AEB,∠CAD=∠ACE+∠AEC,
∵∠AEB+∠AEC=∠BEC,
∴∠BAC=∠ABE+∠ACE+∠BEC.
 (1)证明:由三角形的外角性质得,∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,
(1)证明:由三角形的外角性质得,∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,∵∠BAD+∠CAD=∠BAC,
∴∠BEC=∠BED+∠CED=∠ABE+∠BAD+∠ACE+∠CAD=∠ABE+∠ACE+∠BAC,
即:∠BEC=∠ABE+∠ACE+∠BAC;
(2)解:如图1,点E在BC的下方时,
由四边形的内角和定理得,∠BEC+∠ABE+∠ACE+∠BAC=360°;
如图2,点B在BC的上方时,
由三角形的内角和定理得,∠BAD=∠ABE+∠AEB,∠CAD=∠ACE+∠AEC,
∵∠AEB+∠AEC=∠BEC,
∴∠BAC=∠ABE+∠ACE+∠BEC.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质是解题的关键,难点在于(2)分情况讨论,作出图形更形象直观.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目