题目内容
19.计算:(1)(π-3.14)0-|-3|+($\frac{1}{2}$)-1-(-1)2013
(2)3002-304×296
(3)(2x2)3-4x3(2x3+x2-1)
(4)(x+y-1)2-(x+y-1)(x-y+1)
分析 (1)原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用负整数指数幂法则计算,最后一项利用乘方的意义计算即可得到结果;
(2)原式变形后,利用平方差公式计算即可得到结果;
(3)原式利用幂的乘方与积的乘方运算法则,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(4)原式利用完全平方公式及平方差公式计算,即可得到结果.
解答 解:(1)原式=1-3+2+1=1;
(2)原式=3002-(300+4)×(300-4)=3002-3002+16=16;
(3)原式=8x6-8x6-4x5+4x3=-4x5+4x3;
(4)原式=(x+y-1)(x+y-1-x+y-1)=(x+y-1)(2y-2)=2xy+2y2-2x-4y+2.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10.下列计算正确的是( )
| A. | x2+x4=x6 | B. | x9÷x3=x3 | ||
| C. | x2015+x2015=2x2015 | D. | (x3)3=x6 |
4.为了了解学校开展“尊敬父母,从家务事做起”活动的实施情况,该校抽取初二年级50名学生,调查他们一周(按七天计算)的家务所用时间(单位:小时),得到一组数据,并绘制成下表,请根据该表完成下列各题:
(1)填写频率分布表中未完成的部分;
(2)这组数据的中位数落在什么范围内;
(3)由以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比.
频数分布表
(1)填写频率分布表中未完成的部分;
(2)这组数据的中位数落在什么范围内;
(3)由以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比.
频数分布表
| 分组 | 频数累计 | 频数 | 频率 |
| 0.55~1.05 | 正正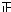 | 14 | 0.28 |
| 1.05~1.55 | 正正正 | 15 | 0.30 |
| 1.55~2.05 | 正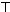 | 7 | 0.14 |
| 2.05~2.55 | 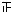 | 4 | 0.08 |
| 2.55~3.05 | 正 | 5 | 0.10 |
| 3.05~3.55 | 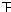 | 3 | 0.06 |
| 3.55~4.05 |  | 2 | 0.04 |
| 合计 | 50 | 1.00 |
8.下列给出的方程中,是二元一次方程的是( )
| A. | xy=5 | B. | 6x=5y | C. | x+$\frac{1}{y}$=6 | D. | 4x+y2=6 |

 在平面直角坐标系xOy中,分别标出点A(4,2)、B(0,6)、C(-1,3)、D、(-2,-3)E(2,-4)、F(3,0)的位置.
在平面直角坐标系xOy中,分别标出点A(4,2)、B(0,6)、C(-1,3)、D、(-2,-3)E(2,-4)、F(3,0)的位置.