题目内容
(1)操作:如图2,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心角为直角的扇形纸板的圆心放在O点处,并将纸板绕O点旋转.求证:正方形ABCD的边被纸板覆盖部分的总长度为定值a.(2)思考:如图1,将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或边长为a的正五边形的中心O点处,并将纸板绕O点旋转.当扇形纸板的圆心角为______时,正三角形的边被纸板覆盖部分的总长度为定值a;如图3,当扇形纸板的圆心角为______时,正五边形的边被纸板覆盖部分的总长度为定值a.(直接填空)
(3)探究:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为______度时,正n边形的边被纸板覆盖部分的总长度为定值a;这时正n边形被纸板覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需证明);若不是定值,请说明理由.
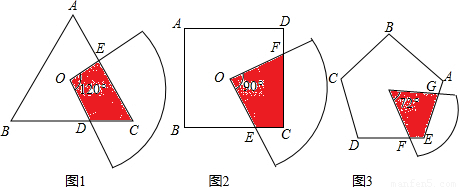
【答案】分析:(1)如图,连接OA、OD,由正方形的性质证得△AOE≌△DOF,有AE=DF,即被纸板覆盖部分的总长度为AF+EA=AF+DF=AD=a为定值.
(2)在等边三角形△ABC中,连接OB,OB,当△OCE≌△OBD时,有OD+OE+CD+CE+OB+OC+BC为定值.此时∠DOE=∠BOC=120°;同理在正五边形中,∠FOG=∠DOE=72°
(3)由(1)(2)可以推得当在扇形纸板的圆心角为 时,正n边形的边被纸板覆盖部分的总长度为定值a;此时正n边形被纸板覆盖部分的面积是定值,等于以正多边形一边与中心构成的三角形的面积,且为
时,正n边形的边被纸板覆盖部分的总长度为定值a;此时正n边形被纸板覆盖部分的面积是定值,等于以正多边形一边与中心构成的三角形的面积,且为 .
.
解答: 解:(1)在正方形ABCD中,设扇形两半径交AB、AD分别于E、F,
解:(1)在正方形ABCD中,设扇形两半径交AB、AD分别于E、F,
作连接OA、OD.
∵O是正方形ABCD的中心,
∴OA=OD,∠OAD=∠ODA=45°,
∴∠AOD=90°.(1分)
∵扇形的圆心角∠EOF=90°,
∴∠AOE+∠AOF=∠DOF+∠AOF,
∴∠AOE=∠DOF,(2分)
∴△AOE≌△DOF(ASA),(3分)
∴AE=DF.(4分)
所以被纸板覆盖部分的总长度为AF+EA=AF+DF=AD=a为定值.(5分)
(2)在等边三角形△ABC中,连接OB,OC,当△OCE≌△OBD时,有OD+OE+CD+CE+OB+OC+BC为定值.此时∠DOE=∠BOC=360°÷3=120°.
同理在正五边形中,∠FOG=∠DOE=360°÷5=72°.
(3)圆心角为 ,(8分)
,(8分)
是定值,被纸板覆盖部分的面积是 .(10分)
.(10分)
故答案为:120°;72°; .
.
点评:本题考查了正多边形的性质,全等三角形的判定和性质.
(2)在等边三角形△ABC中,连接OB,OB,当△OCE≌△OBD时,有OD+OE+CD+CE+OB+OC+BC为定值.此时∠DOE=∠BOC=120°;同理在正五边形中,∠FOG=∠DOE=72°
(3)由(1)(2)可以推得当在扇形纸板的圆心角为
 时,正n边形的边被纸板覆盖部分的总长度为定值a;此时正n边形被纸板覆盖部分的面积是定值,等于以正多边形一边与中心构成的三角形的面积,且为
时,正n边形的边被纸板覆盖部分的总长度为定值a;此时正n边形被纸板覆盖部分的面积是定值,等于以正多边形一边与中心构成的三角形的面积,且为 .
.解答:
 解:(1)在正方形ABCD中,设扇形两半径交AB、AD分别于E、F,
解:(1)在正方形ABCD中,设扇形两半径交AB、AD分别于E、F,作连接OA、OD.
∵O是正方形ABCD的中心,
∴OA=OD,∠OAD=∠ODA=45°,
∴∠AOD=90°.(1分)
∵扇形的圆心角∠EOF=90°,
∴∠AOE+∠AOF=∠DOF+∠AOF,
∴∠AOE=∠DOF,(2分)
∴△AOE≌△DOF(ASA),(3分)
∴AE=DF.(4分)
所以被纸板覆盖部分的总长度为AF+EA=AF+DF=AD=a为定值.(5分)
(2)在等边三角形△ABC中,连接OB,OC,当△OCE≌△OBD时,有OD+OE+CD+CE+OB+OC+BC为定值.此时∠DOE=∠BOC=360°÷3=120°.
同理在正五边形中,∠FOG=∠DOE=360°÷5=72°.
(3)圆心角为
 ,(8分)
,(8分)是定值,被纸板覆盖部分的面积是
 .(10分)
.(10分)故答案为:120°;72°;
 .
.点评:本题考查了正多边形的性质,全等三角形的判定和性质.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目



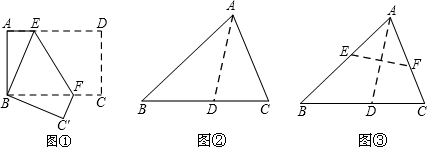
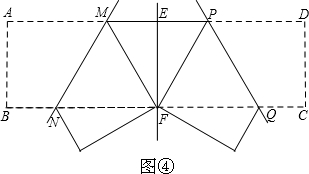
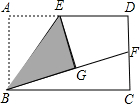 (2011•曲阜市模拟)(1)操作发现
(2011•曲阜市模拟)(1)操作发现