Question

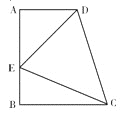
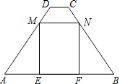
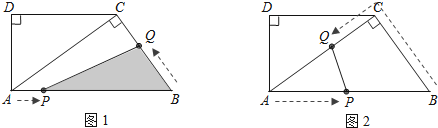
【题目】如图，在梯形中，，，，．点，分别在边，上运动，并保持，，，垂足分别为，．四边形面积的最大值是（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

作梯形ABCD的高DG、CH，先通过梯形两底的差和腰的长求出DG=4，再证明△MEA≌△NFB，得到AE=BF，设AE=x，则EF=7-2x，根据△MEA∽△DGA，求出，根据矩形的面积公式得出S矩形MEFN和x的关系式，化成顶点式即可求出答案．

如图，分别过D，C两点作DG⊥AB于点G，CH⊥AB于点H．

∵AB∥CD，
∴DG=CH，DG∥CH．
∴四边形DGHC为矩形，GH=CD=1．
∵DG=CH，AD=BC，∠AGD=∠BHC=90°，
∴△AGD≌△BHC（HL），
∴

∵在Rt△AGD中，AG=3，AD=5，
∴DG=4．
∵MN∥AB，ME⊥AB，NF⊥AB，
∴∠MEF=90°，
∴ME=NF，ME∥NF，
∴四边形MEFN为矩形．
∵AB∥CD，AD=BC，
∴∠A=∠B．
∵ME=NF，∠MEA=∠NFB=90°，
∴△MEA≌△NFB（AAS）．
∴AE=BF，
设AE=x，则EF=7-2x，
∵∠A=∠A，∠MEA=∠DGA=90°，
∴△MEA∽△DGA，
∴
∴
S矩形MEFN=

当时，ME=

∴四边形MEFN面积的最大值为.

故选:C．