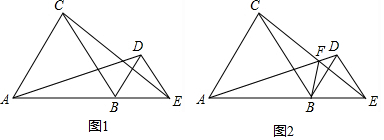
��Ŀ����
15��Rt��ABC�У���C=90�㣬AB=10��AC=6������P��Q�ֱ��A��B������P���˶��ķ�����A��C��B������Q�˶��ķ����Ǵ�B��A������P���˶��ٶ���ÿ��2����λ������Q���˶��ٶ���ÿ��1����λ����P�˶���B��ʱ�˶�ֹͣ����1�����˶�ʱ��Ϊx����APQ�����Ϊy����y����x�ĺ�������ʽ����д��������
��2���������˶������У�ֱ��PQ�ܷ�������ε�����G�����ܣ�д����ʱx��ֵ��
��3���������˶������У�ֱ��PQ�ܷ��������εıߴ�ֱ�����ܣ�д����ʱx��ֵ��
���� ��1���ֵ�P��AC��BC���ϣ��������ε������ʽ��⼴�ɣ�
��2��PQ�����ĵĺ�������PQ��Rt��ACB�ֳ������ȵ������֣������������ε������ʽ��⼴�ɣ�
��3����PQ��AC��PQ��BC��PQ��AB����������жϳ����������ƣ��ó�����ʽ���ɽ���������⼴�ɣ�
��� �⣺��1������P��AC��ʱ������0��x��3��
��BQ=2t��AP=2x��AQ=10-x��
��Rt��ACB��AC=6��AB=10��
��BC=8��
��ͼ1��
����Q��QG��AC��
��QG��BC��
��$\frac{QG}{BC}=\frac{AQ}{AB}$��
��$\frac{QG}{8}=\frac{10-2x}{10}$��
��QG=$\frac{8}{5}��5-x��$��
��y=S��APQ=$\frac{1}{2}$AP��QG=$\frac{1}{2}$��2x��$\frac{8}{5}��5-x��$=-$\frac{8}{5}{x}^{2}+16x$��0��x��3��
����P��BC��ʱ������3��x��7
��BQ=2x��BP=14-2x��AQ=10-x��
��ͼ2������P��PG��AB��
��Rt��BPQ��sinB=$\frac{PG}{BP}=\frac{PG}{14-2x}$
��Rt��ABC��sinB=$\frac{AC}{AB}=\frac{6}{10}=\frac{3}{5}$��
��$\frac{PG}{14-2x}=\frac{3}{5}$
��PG=$\frac{6}{5}��7-x��$��
��y=S��APQ=$\frac{1}{2}$AQ��PG=$\frac{1}{2}$��10-x����$\frac{6}{5}��7-x��$=$\frac{3}{5}{x}^{2}-\frac{51}{5}x+42$����3��x��7��
��2��PQ�����ĵĺ�������PQ��Rt��ACB�ֳ������ȵ������֣�
��S��ABC=$\frac{1}{2}$AC��BC=$\frac{1}{2}$��6��8=24
��y=$\frac{1}{2}$S��ABC=12��
����P��AC��ʱ��-$\frac{8}{5}{x}^{2}+16x$=12
��x=$\frac{10��\sqrt{70}}{2}$��
��0��x��3
��x=$\frac{10-\sqrt{70}}{2}$��
����P��BC��ʱ��$\frac{3}{5}{x}^{2}-\frac{51}{5}x+42$=12��
��x=$\frac{17��\sqrt{89}}{2}$��
��3��x��7
��x=$\frac{17-\sqrt{89}}{2}$��
����x��ֵΪ$\frac{10-\sqrt{70}}{2}$��$\frac{17-\sqrt{89}}{2}$��
��3���������˶������У�P��A��C�ٵ�B��������ʱ��Ϊ��6+8��/2=7s��Q�˶��ľ���Ϊ1��7=7cm��10cm��
��Q��ʼ����AB���ϣ�
��a�� PQ��AC������Q��ʼ����AB���ϣ�����PQ��AC��������P�ض���AC���ϣ�0��x��3����
��Rt��APQ��Rt��ACB��
$\frac{AP}{AC}=\frac{AQ}{AB}$����$\frac{2x}{6}=\frac{10-x}{10}$��x=$\frac{30}{13}$s��3s������Ҫ��
��b�� PQ��BC���루a���ĵ�����ͬ��Ӧ��P����BC���ϣ�3��x��7����
��Rt��BPQ��Rt��BCA��
��$\frac{BP}{BC}=\frac{BQ}{AB}$��
��$\frac{2��7-x��}{8}=\frac{x}{10}$��
��x=5������Ҫ��
��c�� PQ��AB
��P��AC���ϣ�0��x��3����
Ӧ��Rt��AQP��Rt��ACB��������Ϊ��A����
$\frac{AQ}{AC}=\frac{AP}{AB}$��
��$\frac{10-x}{6}=\frac{2x}{10}$��
��x=$\frac{50}{11}$��3s��������Ҫ��
��P��CB���ϣ�3��x��7����
Ӧ��Rt��BQP��Rt��BCA��������Ϊ��A����
$\frac{BQ}{BC}=\frac{BP}{AB}$��
��$\frac{x}{8}=\frac{2��7-x��}{10}$��
��x=$\frac{56}{13}$������Ҫ��
��������������Ҫ���ʱ��Ϊ$\frac{30}{13}$s��5s��$\frac{56}{13}$s��
���� �������������ۺ��⣬��Ҫ�����������ε������ʽ�����������ε����ʺ��ж��������ε����ģ��Ȿ��Ĺؼ���ÿ��������ҳ����������Σ��ѵ��Ƿ������ۣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ���� | B�� | ����3�� | C�� | ����6�� | D�� | ��С��ԭ����$\frac{1}{3}$ |

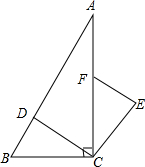 ��ͼ����Rt��ABC�У���ACB=90�㣬��D��F�ֱ���AB��AC�ϣ�CF=CB������CD��CE��CD��CE=CD������EF��
��ͼ����Rt��ABC�У���ACB=90�㣬��D��F�ֱ���AB��AC�ϣ�CF=CB������CD��CE��CD��CE=CD������EF��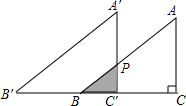 ��ͼ��ʾ��BC=$\sqrt{2}$���Ƚ���ABC���A��B��C�䣬��ȫ�غϣ��ٽ���ABC�̶�����A��B��C����CB���ڵ�ֱ�������ƶ�������ABC���A��B��C����ص����ֵ�����ǡ�ABCһ��ʱ�����A��B��C��ƽ�Ƶľ�����$\sqrt{2}-$1��
��ͼ��ʾ��BC=$\sqrt{2}$���Ƚ���ABC���A��B��C�䣬��ȫ�غϣ��ٽ���ABC�̶�����A��B��C����CB���ڵ�ֱ�������ƶ�������ABC���A��B��C����ص����ֵ�����ǡ�ABCһ��ʱ�����A��B��C��ƽ�Ƶľ�����$\sqrt{2}-$1��