题目内容
7.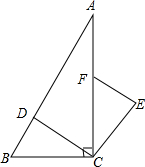 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,CE⊥CD且CE=CD,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,CE⊥CD且CE=CD,连接EF.(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
分析 (1)根据∠ACB=90°、CE⊥CD利用角的计算即可得出∠BCD=∠FCE,再结合CB=CF、CD=CE即可证出△BCD≌△FCE(SAS);
(2)由(1)可得出∠BDC=∠FEC,由EF∥CD利用平行线的性质即可得出∠DCE+∠FEC=180°,再结合CE⊥CD即可得出结论.
解答 (1)证明:∵∠ACB=90°,CE⊥CD,
∴∠BCD+∠DCA=90°=∠DCA+∠FCE,
∴∠BCD=∠FCE.
在△BCD和△FCE中,$\left\{\begin{array}{l}{CB=CF}\\{∠BCD=∠FCE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△FCE(SAS).
(2)解:∵△BCD≌△FCE,
∴∠BDC=∠FEC.
∵EF∥CD,
∴∠DCE+∠FEC=180°,
又∵CE⊥CD,
∴∠FEC=180°-∠DCE=180°-90°=90°,
∴∠BDC=90°.
点评 本题考查了全等三角形的判定与性质、垂直的定义以及平行线的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
17.抛物线y=x2-4x+1的顶点是( )
| A. | (-2,3) | B. | (-2,-3) | C. | (2,3) | D. | (2,-3) |
18.下列代数式$\frac{y}{2}$、x、$\frac{1}{3π}$、$\frac{1}{a-1}$中,是分式的是( )
| A. | $\frac{y}{2}$ | B. | $\frac{1}{a-1}$ | C. | x | D. | $\frac{1}{3π}$ |
12.据宁波市统计局公布的第六次人口普查数据,本市常住人口760.57万人,其中760.57万人用科学记数法表示为( )
| A. | 7.605 7×105人 | B. | 7.605 7×106人 | C. | 7.605 7×107人 | D. | 0.760 57×107人 |
19.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为x cm,面积是S cm2,则S与x的函数关系式为( )
| A. | S=x(20-x) | B. | S=x(20-2x) | C. | S=x(10-x) | D. | S=2x(10-x) |
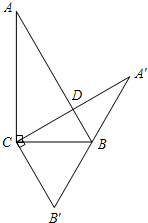 在直角△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C.使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.
在直角△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C.使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.