题目内容
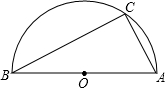
 如图,AB为半圆O的直径,OC⊥AB交⊙O于C,P为BC延长线上一动点,D为AP中点,DE⊥PA,交半径OC于E,连CD.下列结论:①PE⊥AE;②DC=DE;③∠OEA=∠APB;④PC+
如图,AB为半圆O的直径,OC⊥AB交⊙O于C,P为BC延长线上一动点,D为AP中点,DE⊥PA,交半径OC于E,连CD.下列结论:①PE⊥AE;②DC=DE;③∠OEA=∠APB;④PC+ CE为定值.其中正确结论的个数为
CE为定值.其中正确结论的个数为
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:①根据三角形外心的定义得到点E是△ABP的外心,然后利用同弧所对的圆周角等于所对圆心角的一半可以证明PE⊥AE.②根据直径所对的圆周角是直角以及①的结论,可以知道点C和点E在以点D为圆心的同一个圆上,得到DC=DE.③根据垂径定理得到∠AEO= ∠AEB,然后用圆周角定理得到∠APB=∠AEO.④利用③的结论,结合图形,在直角三角形中用余弦进行计算得到PC+
∠AEB,然后用圆周角定理得到∠APB=∠AEO.④利用③的结论,结合图形,在直角三角形中用余弦进行计算得到PC+ CE=
CE= OC,是圆的半径的
OC,是圆的半径的 倍,是一个定值.
倍,是一个定值.
解答: 解:①如图:∵点D是AP的中点,且DE⊥AP,∴DE是AP的垂直平分线,
解:①如图:∵点D是AP的中点,且DE⊥AP,∴DE是AP的垂直平分线,
又AB是半⊙O的直径,OC⊥AB,∴OC是AB的垂直平分线,
∴点E是△ABP的外心,
∵∠ABC=45°,∴∠AEP=90°(同弧所对的圆周角等于它所对圆心角的一半)
∴PE⊥AE,故①正确.
②∵AB是半⊙O的直径,∴∠ACB=90°=∠ACP=∠AEP,
∴点C和点E在以点D为圆心的同一个圆上,∴DC=DE,故②正确.
③由①知点E是△ABP的外心,∴∠APB= ∠AEB=∠AEO,故③正确.
∠AEB=∠AEO,故③正确.
④在直角△APC中,PC=AP•cos∠APC= AE•cos∠AE0=
AE•cos∠AE0= AE•
AE•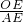 =
= OE,
OE,
∴PC+ CE=
CE= OE+
OE+ CE=
CE= (OE+CE)=
(OE+CE)= OC,
OC,
∴PC+ CE为定值,是⊙O半径的
CE为定值,是⊙O半径的 倍.故④正确.
倍.故④正确.
故选D.
点评:本题考查的是圆周角定理的综合运用,结合图形,利用圆周角定理,对每个选项进行分析,作出正确的判断.
分析:①根据三角形外心的定义得到点E是△ABP的外心,然后利用同弧所对的圆周角等于所对圆心角的一半可以证明PE⊥AE.②根据直径所对的圆周角是直角以及①的结论,可以知道点C和点E在以点D为圆心的同一个圆上,得到DC=DE.③根据垂径定理得到∠AEO=
 ∠AEB,然后用圆周角定理得到∠APB=∠AEO.④利用③的结论,结合图形,在直角三角形中用余弦进行计算得到PC+
∠AEB,然后用圆周角定理得到∠APB=∠AEO.④利用③的结论,结合图形,在直角三角形中用余弦进行计算得到PC+ CE=
CE= OC,是圆的半径的
OC,是圆的半径的 倍,是一个定值.
倍,是一个定值.解答:
 解:①如图:∵点D是AP的中点,且DE⊥AP,∴DE是AP的垂直平分线,
解:①如图:∵点D是AP的中点,且DE⊥AP,∴DE是AP的垂直平分线,又AB是半⊙O的直径,OC⊥AB,∴OC是AB的垂直平分线,
∴点E是△ABP的外心,
∵∠ABC=45°,∴∠AEP=90°(同弧所对的圆周角等于它所对圆心角的一半)
∴PE⊥AE,故①正确.
②∵AB是半⊙O的直径,∴∠ACB=90°=∠ACP=∠AEP,
∴点C和点E在以点D为圆心的同一个圆上,∴DC=DE,故②正确.
③由①知点E是△ABP的外心,∴∠APB=
 ∠AEB=∠AEO,故③正确.
∠AEB=∠AEO,故③正确.④在直角△APC中,PC=AP•cos∠APC=
 AE•cos∠AE0=
AE•cos∠AE0= AE•
AE•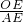 =
= OE,
OE,∴PC+
 CE=
CE= OE+
OE+ CE=
CE= (OE+CE)=
(OE+CE)= OC,
OC,∴PC+
 CE为定值,是⊙O半径的
CE为定值,是⊙O半径的 倍.故④正确.
倍.故④正确.故选D.
点评:本题考查的是圆周角定理的综合运用,结合图形,利用圆周角定理,对每个选项进行分析,作出正确的判断.

练习册系列答案
相关题目
 为D,AD=a,DB=b.
为D,AD=a,DB=b.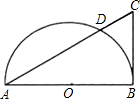 如图,AB为半圆O的直径,CB切半圆于点B,AC交半圆于点D,若CD=1,AD=3,则⊙O半径的长为
如图,AB为半圆O的直径,CB切半圆于点B,AC交半圆于点D,若CD=1,AD=3,则⊙O半径的长为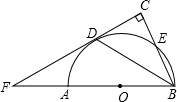 C,直线CD交BA的延长线于点F.
C,直线CD交BA的延长线于点F. 如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有
如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有