Question

在平面直角坐标系中，已知点A（3，0），B（0，4），将△BOA绕点A按顺时针方向旋转得△CDA，连接OD．当∠DOA=∠OBA时，直线CD的解析式为　　．

Answer 1

y=﹣x+4【考点】一次函数综合题．

【专题】综合题．

【分析】由旋转的性质得到三角形BOA与三角形CDA全等，再由已知角相等，以及公共角，得到三角形AOM与三角形AOB相似，确定出OD与AB垂直，再由OA=DA，利用三线合一得到AB为角平分线，M为OD中点，利用SAS得到三角形AOB与三角形ABD全等，得出AD垂直于BC，进而确定出B，D，C三点共线，求出直线OD解析式，与直线AB解析式联立求出M坐标，确定出D坐标，设直线CD解析式为y=mx+n，把B与D坐标代入求出m与n的值，即可确定出解析式．

【解答】解：∵△BOA绕点A按顺时针方向旋转得△CDA，

∴△BOA≌△CDA，

∵∠DOA=∠OBA，∠OAM=∠BAO，

∴△AOM∽△ABO，

∴∠AMO=∠AOB=90°，

∴OD⊥AB，

∵AO=AD，

∴∠OAM=∠DAM，

在△AOB和△ABD中，

，

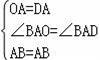
∴△AOB≌△ABD（SAS），

∴OM=DM，

∴△ABD≌△ACD，

∴∠ADB=∠ADC=90°，

∴B，D，C三点共线，

设直线AB解析式为y=kx+b，

把A与B坐标代入得：，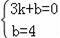

解得：，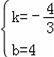

∴直线AB解析式为y=﹣x+4，

∴直线OD解析式为y=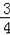x，

联立得：，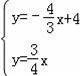

解得：，即M（，），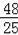

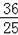
∵M为线段OD的中点，

∴D（，），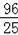

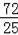
设直线CD解析式为y=mx+n，

把B与D坐标代入得：，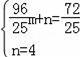

解得：m=﹣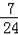，n=4，

则直线CD解析式为y=﹣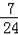x+4．

故答案为：y=﹣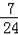x+4

【点评】此题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，一次函数与坐标轴的交点，两直线的交点坐标，坐标与图形性质，以及旋转的性质，得出B，D，C三点共线是解本题的关键．