题目内容
已知反比例函数y=
(k≠0)的图象经过点(1,-k+2).
(1)求这个反比例函数的解析式;
(2)若(a,y1),(a+1,y2)是这个反比例函数图象上的两个点,请比较y1、y2的大小,并说明理由.
| k |
| x |
(1)求这个反比例函数的解析式;
(2)若(a,y1),(a+1,y2)是这个反比例函数图象上的两个点,请比较y1、y2的大小,并说明理由.
考点:待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征
专题:
分析:(1)把点(1,-k+2)代入函数解析式,列出关于k的方程,通过解方程来求k的值即可;
(2)反比例函数的y=
的图象在每一个象限内都是减函数.需要分类讨论:分a>0,-1<a<0,a<-1三种情况.
(2)反比例函数的y=
| 1 |
| x |
解答:解:(1)∵反比例函数y=
(k≠0)的图象经过点(1,-k+2),
∴-k+2=
,
解得 k=1.
∴这个反比例函数的解析式是y=
;
(2)①当a>0时,则a<a+1,
∵反比例函数y=
的图象在第一象限内是减函数,
∴y1>y2;
②当-1<a<0时,则a+1>0,
由图象知y1<y2;
当a<-1时,则a<a+2,
∵反比例函数y=
的图象在第三象限内是减函数,
∴y1>y2.
| k |
| x |
∴-k+2=
| k |
| 1 |
解得 k=1.
∴这个反比例函数的解析式是y=
| 1 |
| x |
(2)①当a>0时,则a<a+1,
∵反比例函数y=
| 1 |
| x |
∴y1>y2;
②当-1<a<0时,则a+1>0,
由图象知y1<y2;
当a<-1时,则a<a+2,
∵反比例函数y=
| 1 |
| x |
∴y1>y2.
点评:本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征.解题时,需要熟练掌握反比例函数图象的性质.

练习册系列答案
相关题目
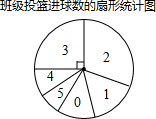 小华班上比赛投篮,每人5次,如图是班上所有学生的投篮进球数的扇形统计图,则下列关于班上所有学生投进球数的统计量正确的是( )
小华班上比赛投篮,每人5次,如图是班上所有学生的投篮进球数的扇形统计图,则下列关于班上所有学生投进球数的统计量正确的是( )| A、中位数是3个 |
| B、中位数是2.5个 |
| C、众数是2个 |
| D、众数是5个 |
 如图,该几何体的哪个视图是轴对称图形( )
如图,该几何体的哪个视图是轴对称图形( )| A、左视图 | B、主视图 |
| C、俯视图 | D、左视图和主视图 |
已知整数x满足是不等式组
,则x的算术平方根为( )
|
| A、2 | ||
| B、±2 | ||
C、
| ||
| D、4 |
 小明同学将直角三角形直角顶点置于平面直角坐标系的原点O,两直角边与抛物线y=-
小明同学将直角三角形直角顶点置于平面直角坐标系的原点O,两直角边与抛物线y=- 如图,一次函数y=-
如图,一次函数y=-