Question

【题目】阅读理解：

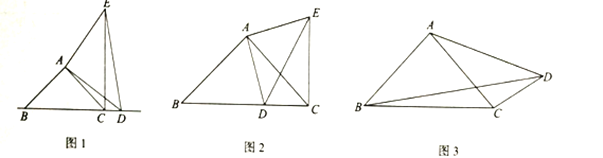
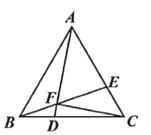
如图所示，在正中，、分别在、边上，若，则．小强是这样论证的：

∵是正三角形，∴．∴．

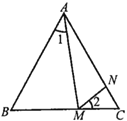
又因为，，∴．∴．

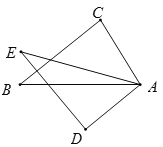
（1）类比应用：如图所示，将阅读理解中的正三角形换成正四边形，、分别为、上的点，类似地：若__________，则．请你用小强的证明方法论证．

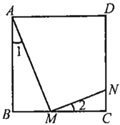
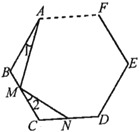
（2）拓展延伸：请你将上述命题推广到一般，如图所示，…是正边形．

写出命题：______________________________________．

Answer 1

【答案】（1）90°，证明见解析；（2）在正边形…中，、分别为、上的点，若，则．证明见解析．

【解析】

（1）先根据正方形的性质、三角形的外角性质得出，再根据角的和差可得，从而即可得证；

（2）参照题（1）、（2）即可写出命题；再根据正n边形的性质、三角形的外角性质得出，再根据角的和差可得，从而即可得证．

（1），证明过程如下：

四边形是正四边形

∴

∴

又，

∴

∴；

（2）在正n边形…中，、分别为、上的点，若，则．证明过程如下：

n边形…是正n边形

∴

∴

又，

∴

∴．