题目内容
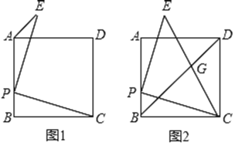
【题目】已知:如图,六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可 得六边形 ABCDEF 中必有两条边是平行的.

(1)根据图形写出你的猜想: ∥ ;
(2)请证明你在(1)中写出的猜想.
【答案】(1)AF∥CD;(2)见解析;
【解析】
(1)根据多边形的内角和以及已知条件求出∠A+∠B+∠C=360°,连接AC,根据三角形的内角和等于180°可以求出∠FAC+∠ACD=180°,然后根据同旁内角互补,两直线平行即可证明AF∥CD;
(2)根据(1)中的分析思路写出证明过程即可.
(1)猜想:AF∥CD;
(2)证明:如图,连接AC,

∵∠A+∠B+∠C=∠D+∠E+∠F,
∴∠A+∠B+∠C=(62)180°÷2=360°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠FAC+∠ACD=360°180°=180°,
∴AF∥CD.

练习册系列答案
相关题目
【题目】某学校开展了“好读书、读好书”的课外阅读活动,为了解同学们的读书情况,从全校随机抽取了![]() 名学生,并统计它们平均每天的课外阅读时间(单位:
名学生,并统计它们平均每天的课外阅读时间(单位:![]() ),然后利用所得数据绘制成如下不完整的统计图表.
),然后利用所得数据绘制成如下不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间 | 频数 | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
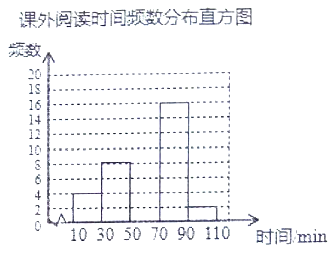
请根据图表中提供的信息回答下列问题:
(1)填空:![]() __________,
__________,![]() __________;
__________;
(2)将频数分布直方图补充完整;
(3)若全校有![]() 名学生,估计该校有多少名学生平均每天的课外阅读时间不少于
名学生,估计该校有多少名学生平均每天的课外阅读时间不少于![]() ?
?