题目内容
等腰直角三角形的面积为8,则斜边长为分析:根据等腰直角三角形的面积公式(S△ABC=
AC•BC=8)求得AC与BC的数量关系,再由勾股定理求得直角三角形的斜边AB与两直角边的数量关系.
| 1 |
| 2 |
解答: 解:已知如图所示:
解:已知如图所示:
AC=BC,AC⊥BC,S△ABC=8.
∵S△ABC=
AC•BC,
∴
AC•BC=8,即AC•BC=16;
∵AC=BC,AC2+BC2=AB2,
∴AB2=32,
∴AB=±4
,
又∵AB>0,
∴AB=4
.
 解:已知如图所示:
解:已知如图所示:AC=BC,AC⊥BC,S△ABC=8.
∵S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∵AC=BC,AC2+BC2=AB2,
∴AB2=32,
∴AB=±4
| 2 |
又∵AB>0,
∴AB=4
| 2 |
点评:解答本题的关键是找对等腰直角三角形的斜边与两直角边的数量关系.

练习册系列答案
相关题目
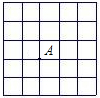 如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为
如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为| 5 |
| 2 |
| A、4个 | B、8个 |
| C、12个 | D、16个 |
 如图,在正方形上连接等腰直角三角形和正方形,无限重复同一过程,第一个正方形的边长为1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2,…,第n个正方形与第n个等腰直角三角形的面积和为Sn,猜想出Sn与n的关系
如图,在正方形上连接等腰直角三角形和正方形,无限重复同一过程,第一个正方形的边长为1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2,…,第n个正方形与第n个等腰直角三角形的面积和为Sn,猜想出Sn与n的关系 (2012•郑州模拟)如图,线段AB=8cm,点C是AB上任意一点(不与点A、B重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形(△AMC和△CNB),则当BC=
(2012•郑州模拟)如图,线段AB=8cm,点C是AB上任意一点(不与点A、B重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形(△AMC和△CNB),则当BC= 如图,以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第2012个等腰直角三角形的面积S2012=
如图,以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第2012个等腰直角三角形的面积S2012=