题目内容
 (2012•郑州模拟)如图,线段AB=8cm,点C是AB上任意一点(不与点A、B重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形(△AMC和△CNB),则当BC=
(2012•郑州模拟)如图,线段AB=8cm,点C是AB上任意一点(不与点A、B重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形(△AMC和△CNB),则当BC=4
4
cm时,两个等腰直角三角形的面积和最小.分析:作MD⊥AC,NE⊥BC,设AC=xcm,则BC=(8-x)cm,将两三角形面积之和表示为S=
•x•
x+
•(8-x)•
(8-x),转化为二次函数的最值问题解答.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:作MD⊥AC,NE⊥BC,
解:作MD⊥AC,NE⊥BC,
∵△AMC和△CNB是等腰直角三角形,
∴DC=MD,EB=NE,
∴设AC=xcm,则BC=(8-x)cm,
∴两三角形面积之和为S=
•x•
x+
•(8-x)•
(8-x)
=
x2+
(64+x2-16x)
=
x2+16+
x2-4x
=
x2-4x+16
当AC=-
=4,
即BC=8-4=4cm时,两个等腰三角形的面积最小.
 解:作MD⊥AC,NE⊥BC,
解:作MD⊥AC,NE⊥BC,∵△AMC和△CNB是等腰直角三角形,
∴DC=MD,EB=NE,
∴设AC=xcm,则BC=(8-x)cm,
∴两三角形面积之和为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 2 |
当AC=-
| -4 | ||
2×
|
即BC=8-4=4cm时,两个等腰三角形的面积最小.
点评:本题考查了等腰直角三角形和二次函数的最值,将三角形的面积问题转化为二次函数的最值问题是解题的关键.

练习册系列答案
相关题目
 (2012•郑州模拟)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,若∠1=26°,则∠2的度数为
(2012•郑州模拟)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,若∠1=26°,则∠2的度数为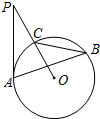 (2012•郑州模拟)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧
(2012•郑州模拟)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧
 (2012•郑州模拟)郑州地铁一号线将于2013年底建成,它的通车将给市民的出行方式带来一些新变化.小王和小林准备利用课余时间,以问卷的方式对郑州市民的出行方式进行调查.如图是郑州地铁一号线图(部分),小王和小林分别从郑州火车站、二七广场站、市体育馆站这三站中,随机选取一站向其周围的人群进行问卷调查,则小王选取的站点与小林选取的站点相邻的概率是
(2012•郑州模拟)郑州地铁一号线将于2013年底建成,它的通车将给市民的出行方式带来一些新变化.小王和小林准备利用课余时间,以问卷的方式对郑州市民的出行方式进行调查.如图是郑州地铁一号线图(部分),小王和小林分别从郑州火车站、二七广场站、市体育馆站这三站中,随机选取一站向其周围的人群进行问卷调查,则小王选取的站点与小林选取的站点相邻的概率是 (2012•郑州模拟)已知二次函数y=ax2+bx-2的图象经过点A(1,0)及B(-2,0)两点.
(2012•郑州模拟)已知二次函数y=ax2+bx-2的图象经过点A(1,0)及B(-2,0)两点.