题目内容
14. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′;
(2)四边形ABB′A′的周长为$8+2\sqrt{5}$;
(3)四边形ABCA′的面积为$\frac{17}{2}$;
(4)在直线l上找一点P,使PA+PB的长最短,则这个最短长度为$\sqrt{17}$.
分析 (1)根据题意作出图形即可;
(2)根据勾股定理即可得到结论;
(3)根据三角形的面积公式即可得到结论;
(4)作出图形,根据勾股定理求得结果即可.
解答 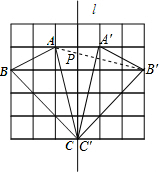 解:(1)如图所示,△A′B′C′即为所求;
解:(1)如图所示,△A′B′C′即为所求;
(2)四边形ABB′A′的周长=AB+BB′+A′B′+AA′=$\sqrt{{2}^{2}+{1}^{2}}$+6+$\sqrt{{2}^{2}+{1}^{2}}$+2=$8+2\sqrt{5}$;
故答案为:$8+2\sqrt{5}$;
(3)四边形ABCA′的面积=4×4-$\frac{1}{2}×$2×1-$\frac{1}{2}×$1×4-$\frac{1}{2}×$3×3=$\frac{17}{2}$;
故答案为:$\frac{17}{2}$;
(4)连接AB′交直线l与点P,
则PA+PB长的最短值=AB′,
∴AB′=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$;
故答案为:$\sqrt{17}$.
点评 本题考查了轴对称-最短路线问题,勾股定理,作图-轴对称变换,正确的理解题意是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |
9.金秋十月,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如表:
(1)如果他批发80千克太湖蟹,则他在A 家批发需要4416元,在B家批发需要4380元;
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
19.函数y=x2-4x+3与y轴的交点为( )
| A. | (1,1) | B. | (0,3) | C. | (-1,2) | D. | (2,-1) |
6.近年来,全国房价不断上涨,某县2014年2月份的房价平均每平方米为3600元,比2012年同期的房价平均每平方米上涨了500元,假设这两年该县房价的平均增长率均为x,则关于x 的方程为( )
| A. | (1+x)2=500 | B. | 500(1+x)2=3600 | ||
| C. | (3600-500)(1+x)=3600 | D. | (3600-500)(1+x)2=3600 |
3.下列合并同类项中,正确的是( )
| A. | 3x+2y=6xy | B. | 2a2+3a3=5a3 | C. | 3mn-3nm=0 | D. | 7x-5x=2 |
 已知抛物线的不等式为y=-x2+6x+c.
已知抛物线的不等式为y=-x2+6x+c.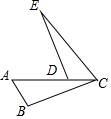 已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.