题目内容
18、O为平面上一点，过点O在这个平面上引2007条不同的直线 l1，l2，l3，…，l2007，则可形成
4026042
对以O为顶点的对顶角．分析：我们知道，每两条直线相交，能形成2对对顶角，本题的关键在于推导出n条这样的直线能形成多少对对顶角．
解答：解：n=3时，有2×3对；
n=4时，有3×4对；
…，
n条直线应有n（n-1）对，即n条直线可产生对顶角n（n-1）对．
当n=2007时，可形成2007（2007-1）=4026042对对顶角．
故答案为：4026042．
n=4时，有3×4对；
…，
n条直线应有n（n-1）对，即n条直线可产生对顶角n（n-1）对．
当n=2007时，可形成2007（2007-1）=4026042对对顶角．
故答案为：4026042．
点评：本题考查了对顶角的定义及规律的探寻，总结并找出对顶角对数的公式是解题的关键．
练习册系列答案
相关题目
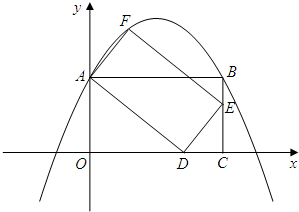、n的代数式表示该抛物线；若不存在，请说明理由．
中，点
关于
轴的对称点为
，
与
，将△
沿
翻折后，点
处．
、
，点
为线段
轴的平行线，交抛物线于点
．
为等腰梯形时，求出点