题目内容
某菱形的两条对角线长都是方程x2-6x+8=0的根,则该菱形的周长为 .
考点:菱形的性质,解一元二次方程-因式分解法
专题:
分析:由菱形ABCD的两条对角线长分别是方程x2-6x+8=0的两根,可求得菱形ABCD的两条对角线长分别是2与4,然后由菱形的性质与勾股定理,即可求得菱形周长.
解答:解:∵x2-6x+8=0,
∴(x-2)(x-4)=0,
解得:x1=2,x2=4,
∵菱形ABCD的两条对角线长分别是方程x2-6x+8=0的两根,
∴菱形ABCD的两条对角线长分别是2与4,
设菱形ABCD的两条对角线相交于O,
∴AC⊥BD,OA=
AC=2,OB=
BD=1,
∴AB=
=
,
∴菱形周长为:4AB=4
.
故答案为:4
.

∴(x-2)(x-4)=0,
解得:x1=2,x2=4,
∵菱形ABCD的两条对角线长分别是方程x2-6x+8=0的两根,
∴菱形ABCD的两条对角线长分别是2与4,
设菱形ABCD的两条对角线相交于O,
∴AC⊥BD,OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
| 5 |
∴菱形周长为:4AB=4
| 5 |
故答案为:4
| 5 |
点评:此题考查了菱形的性质与勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A、36(1-x)2=36-25 |
| B、36(1-x)2=25 |
| C、36(1-2x)=25 |
| D、36(1-x2)=25 |
 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1:5,则
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1:5,则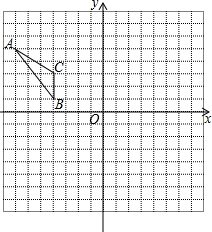 如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.