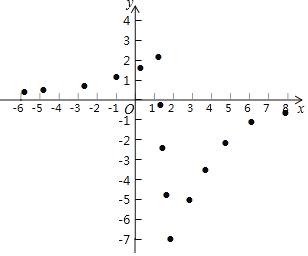题目内容
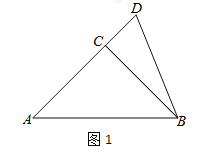
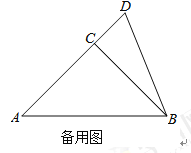
【题目】如图,![]() 中,
中,![]() ,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
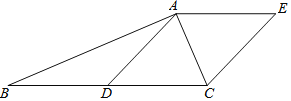
(1)求证:四边形ADCE是菱形;
(2)如果![]() ,
,![]() ,写出求菱形ADCE的面积的思路.
,写出求菱形ADCE的面积的思路.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)先证明四边形ADCE是平行四边形,再由直角三角形斜边上的中线性质得出AD=CD,即可得出结论;
(2)由中线的性质得出△ABC的面积=2△ACD的面积,由菱形的性质得出菱形ADCE的面积=2△ACD的面积,得出菱形ADCE的面积=△ABC的面积,由三角函数得出AB=3a,即可求出答案.
(1)∵AE∥BC,AE=CD,
∴四边形ADCE是平行四边形.
∵∠BAC=90°,D是BC边的中点,
∴AD=BD=CD.
∴平行四边形ADCE是菱形.
(2)∵D是BC边的中点,
∴△ABC的面积=2△ACD的面积,
∵四边形ADCE是菱形,
∴菱形ADCE的面积=2△ACD的面积,
∴菱形ADCE的面积=△ABC的面积,
∵∠BAC=90°,![]() ,
,![]() ,
,
∴AB=3AC=3a,
∴菱形ADCE的面积![]() .
.

【题目】某班数学活动小组测量吉林市“世纪之舟”的高度.他们制定了测量方案,并利用课余时间完成了实地测景,测量项目及数据如下表:
项目 | 内容 | |||
课题 | 测量吉林市“实际之舟”的高度 | |||
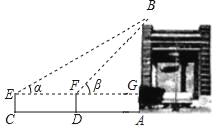
示意图 |
| 如图,用测角仪在 | ||
测量数据 |
|
|
| 测角仪 |
|
| 50米 | 1.5米 | |
… | … | |||
请你根据活动小组测得的数据,求世纪之舟的高![]() (结果保留小数点后一位).
(结果保留小数点后一位).
(参考数据:![]() ,
,![]() ,
,![]() )
)
【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量y(千克)与每千克售价x(元)的关系如表所示
每千克售价x(元) | 25 | 30 | 40 |
每周销售量y(千克) | 240 | 200 | 150 |
(1)写出每周销售量y(千克)与每千克售价x(元)的函数关系式;
(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否到达每周获利1200元?说明理由.