题目内容
已知：如图，在平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，平行四边形ABCD的周长为28，面积为40，AB：AD=4：3．
求：（1）DE的长；（2）sin∠EDF的值．
分析：（1）因为平行四边形的周长为28，且相邻两边之比为4比3，所以可求出每边的长，又面积一定，即可求出边上的高．
（2）在四边形DEBF中，已知两个直角，所以∠B+∠EDF=180°，而∠A+∠B=180°即sin∠EDF的值也就时sinA，在直角△AED中，sinA可通过已知的AD和AE求出．
（2）在四边形DEBF中，已知两个直角，所以∠B+∠EDF=180°，而∠A+∠B=180°即sin∠EDF的值也就时sinA，在直角△AED中，sinA可通过已知的AD和AE求出．
解答：解：（1）平行四边形ABCD中，AB=CD，AD=BC
∵平行四边形ABCD的周长为28
∴AB+AD=14
又AB：AD=4：3
∴AB=8，AD=6，
又S?ABCD=AB×DE=40
∴DE=5
（2）在四边形DEBF中，∠EDF+∠DEB+∠B+∠BFD=360°
又DE⊥AB，DF⊥BC
∴∠EDF+∠B=180°
又在平行四边形ABCD中∠A+∠B=180°
∴∠EDF=∠A
在RT△ADE中，sinA=
=
∴sin∠EDF=sinA=
∵平行四边形ABCD的周长为28
∴AB+AD=14
又AB：AD=4：3
∴AB=8，AD=6，
又S?ABCD=AB×DE=40
∴DE=5
（2）在四边形DEBF中，∠EDF+∠DEB+∠B+∠BFD=360°
又DE⊥AB，DF⊥BC
∴∠EDF+∠B=180°
又在平行四边形ABCD中∠A+∠B=180°
∴∠EDF=∠A
在RT△ADE中，sinA=
| DE |
| AD |
| 5 |
| 6 |
∴sin∠EDF=sinA=
| 5 |
| 6 |
点评：此题主要考查了平行四边形的基本性质以及三角函数的应用，属于中等难度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
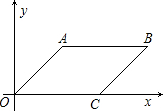如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，