题目内容
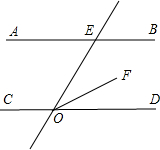如图所示，已知∠OEB=130°，∠FOD=25°，OF平分∠EOD，试说明AB∥CD．
证明：∵OF平分∠EOD，
∴∠FOD=
∠EOD；
∵∠FOD=25°，
∴∠EOD=50°；
又∵∠OEB=130°，
∴∠OEB+∠EOD=180°，
∴AB∥CD（同旁内角互补，两直线平行）．
分析：根据角平分线的定义先求出∠EOD的度数，再利用同旁内角互补，两直线平行可证明AB∥CD．
点评：此题主要考查了角平分线的定义和同旁内角互补，两直线平行的判定定理．
∴∠FOD=
∠EOD；∵∠FOD=25°，
∴∠EOD=50°；
又∵∠OEB=130°，
∴∠OEB+∠EOD=180°，
∴AB∥CD（同旁内角互补，两直线平行）．
分析：根据角平分线的定义先求出∠EOD的度数，再利用同旁内角互补，两直线平行可证明AB∥CD．
点评：此题主要考查了角平分线的定义和同旁内角互补，两直线平行的判定定理．
练习册系列答案
快乐5加2金卷系列答案
相关题目
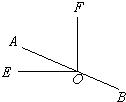13、如图所示，已知OE⊥OF，直线AB过点O，则∠BOF-∠AOE=
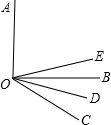如图所示，已知OE是∠AOC的平分线，OD是∠BOC的平分线．
如图所示，已知OE⊥OF，直线AB经过点O，若∠AOF=2∠AOE，则∠BOF=
如图所示，已知OE是∠AOC的平分线，OD是∠BOC的平分线．