Question

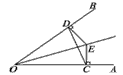
如图所示，已知OE是∠AOC的平分线，OD是∠BOC的平分线．
（1）若∠AOC=120°，∠BOC=β，求∠DOE；

 

；
（2）若∠AOC=α，∠BOC=β（α＞β），求∠BOE．

 

．

Answer 1

分析：根据角平分线的性质计算．

解答：解：（1）∠AOC=120°，
∴∠COE=60°（角平分线定义），
∵∠BOC=β，
∴∠COD=

1

2

β（角平分线定义），
∴∠DOE=60°-

1

2

β；

（2）∵∠AOC=α，OE是∠AOC的平分线，且∠BOC=β（α＞β），
∴∠COE=

1

2

α（角平分线定义）．
∴∠BOE=∠COE-∠BOC=

1

2

α-β．

点评：此题主要考查了角平分线定义．由角平分线的定义，易求该角的度数．