题目内容
 如图,点A、B、C在⊙O上,若∠BAC=24°,则∠OBC=
如图,点A、B、C在⊙O上,若∠BAC=24°,则∠OBC=考点:圆周角定理
专题:
分析:由∠BAC=24°,根据圆周角定理,可求得∠BOC的度数,又由等腰三角形的性质,即可求得答案.
解答:解:∵∠BAC=24°,
∴∠BOC=2∠BAC=48°,
∵OB=OC,
∴∠OBC=∠OCB=
=66°.
故答案为:66.
∴∠BOC=2∠BAC=48°,
∵OB=OC,
∴∠OBC=∠OCB=
| 180°-∠BOC |
| 2 |
故答案为:66.
点评:此题考查了圆周角定理以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
在数轴上表示整数的点称为整数点,某数轴的单位长度是1cm,若在这个数轴上随意画出一条长2015cm的线段AB,则被线段AB盖住的整数有( )
| A、2012个或2013个 |
| B、2013个或2014个 |
| C、2014个或2015个 |
| D、2015个或2016个 |
下列说法正确的是( )
| A、绝对值大的数一定大于绝对值小的数 |
| B、任何有理数的绝对值都不可能是负数 |
| C、任何有理数的相反数都是正数 |
| D、有理数的绝对值都是正数 |
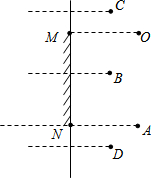 如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有
如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有