Question

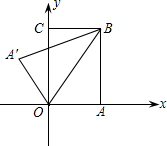如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若OB=

5

，tan∠BOC=

1

2

，则点A′的坐标为

 

．

Answer 1

考点：翻折变换（折叠问题）,坐标与图形性质

专题：

分析：如图，作辅助线；根据题意首先求出AB、BC的长度；借助面积公式求出A′D、OD的长度，即可解决问题．

解答：解：如图，过点A′作A′D⊥x轴与点D；
设A′D=λ，OD=μ；
∵四边形ABCD为矩形，
∴∠OAB=∠OCB=90°；四边形ABA′D为梯形；
设AB=OC=γ，BC=AO=ρ；
∵OB=

5

，tan∠BOC=

1

2

，
∴

γ2+ρ2=( 5 )2 ρ γ = 1 2

，
解得：γ=2，ρ=1；
由题意得：A′O=AO=1；△ABO≌△A′BO；
由勾股定理得：λ²+μ²=1①，
由面积公式得：

1

2

λμ+2×

1

2

×2×1=

1

2

(λ+2)×(μ+1)②；
联立①②并解得：λ=

4

5

，μ=

3

5

．
故答案为（-

3

5

，

4

5

）．

点评：该题以平面直角坐标系为载体，以翻折变换为方法构造而成；综合考查了矩形的性质、三角函数的定义、勾股定理等几何知识点；对分析问题解决问题的能力提出了较高的要求．