题目内容
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
(1)y=-2x2+6.y=- .(2)点(-1,4)既在y=-2x2+6图象上,也在y=-
.(2)点(-1,4)既在y=-2x2+6图象上,也在y=- 图象上.
图象上.
【解析】
试题分析:(1)将点P(1,-2a)代入二次函数y=ax2+6,组成方程组即可求出a的值,从而求出点P关于x轴的对称点坐标,代入解析式即可求出k的值,从而得到函数解析式;
(2)将点(-1,4)分别代入两个函数的解析式,若同时成立,则否同时在(1)中的两个函数图象上.
试题解析:(1)∵点P(1,-2a)在二次函数y=ax2+6的图象上,
∴-2a=a+6, a=-2.
∴点P为(1,4),所求二次函数解析式为y=-2x2+6.
点P关于x轴对称点的坐标为(1,-4),
∴k=-4,所求反比例函数解析式为y=- .
.
(2)点(-1,4)既在y=-2x2+6图象上,也在y=- 图象上.
图象上.
考点:1.二次函数图象上点的坐标特征;2.反比例函数图象上点的坐标特征.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
某射击运动员在相同条件下的射击160次,其成绩记录如下:
射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
射中9环以上的次数 | 15 | 33 | 63 | 79 | 97 | 111 | 130 | |
射中9环以上的频率 | 0.75 | 0.83 | 0.80 | 0.79 | 0.79 | 0.79 | 0.81 |
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.

 知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为20°,则∠α的度数为( )
知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为20°,则∠α的度数为( )
 与二次函数
与二次函数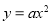 的图象的公共点在第三象限,则一次函数
的图象的公共点在第三象限,则一次函数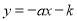 的图象不经过
的图象不经过