题目内容
12.解方程组$\left\{\begin{array}{l}{x+y+z=4}\\{2x-y+z=3}\\{3x-2y-3z=-5}\end{array}\right.$.分析 先化为二元一次方程组,再化为一元一次方程,求解即可.
解答 解:$\left\{\begin{array}{l}{x+y+z=4①}\\{2x-y+z=3②}\\{3x-2y-3z=-5③}\end{array}\right.$,
①+②,得3x+2z=7④,
①×2+③,得5x-z=3⑤,
④+⑤×2,得13x=13,
解得x=1,
把x=1代入⑤得z=2,
把x=1,z=2代入①得,y=1,
∴原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$.
点评 本题考查二元一次方程组和三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解二元一次方程组较简单.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
4.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
| A. | 北偏西30° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏西60° |
17.在数-3,0,2,π四个数中,最大的是( )
| A. | -3 | B. | 0 | C. | 2 | D. | π |
 如图,在菱形ABCD中,DE⊥AB,sinA=$\frac{4}{5}$,BE=2,则tan∠BDE的值是$\frac{1}{2}$.
如图,在菱形ABCD中,DE⊥AB,sinA=$\frac{4}{5}$,BE=2,则tan∠BDE的值是$\frac{1}{2}$.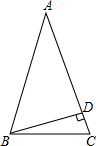 如图,△ABC中,AB=AC,BD⊥AC于点D,∠C=75°,BD=3,求△ABC的面积.
如图,△ABC中,AB=AC,BD⊥AC于点D,∠C=75°,BD=3,求△ABC的面积.