题目内容
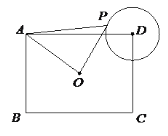
【题目】如图,已知![]() ,将一个直角的顶点置于点
,将一个直角的顶点置于点![]() ,并将它绕着点
,并将它绕着点![]() 旋转,两条直角边分别交射线
旋转,两条直角边分别交射线![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,联结
,联结![]() 交
交![]() 于点
于点![]() ,设
,设![]() .
.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)若![]() ,求
,求![]() 关于
关于![]() 的函数关系式及定义域;
的函数关系式及定义域;
(3)旋转过程中,若![]() ,求此时
,求此时![]() 的长.
的长.
【答案】(1)![]() ;(2)y=
;(2)y=![]() x+4(0≤x≤
x+4(0≤x≤![]() );(3)
);(3)![]() .
.
【解析】
(1)首先证明,∠CBE=90°,∠BCE=30°,根据tan30°=![]() ,即可解决问题.
,即可解决问题.
(2)如图2中,作DM⊥BC于M.只要证明△DCM∽△CEB,得![]() ,由此即可解决问题.
,由此即可解决问题.
(3)先证明∠EDA=∠EDC,由EA⊥DA,EC⊥DC,推出EA=EC=x+3,在Rt△BCE中,根据EC2=BE2+BC2,列出方程即可解决问题.
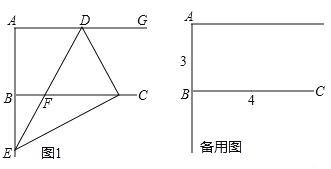
解:(1)如图1中,
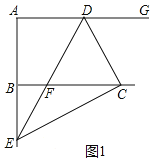
∵∠DCE=90°,∠DCF=60°,
∴∠BCE=30°,
∵AB⊥BC,
∴∠CBE=90°,
∴tan30°=![]() ,
,
∴![]()
∴BE=![]() .
.
(2)如图2中,作DM⊥BC于M.
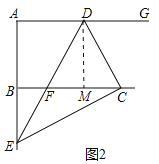
∵AG∥BC,AB⊥BC,
∴AG⊥AB,
∴∠A=∠ABM=∠DMB=90°,
∴四边形ABMD是矩形,
∴BM=AD=y,AB=DM=3,CM=4-y,
∵∠DCM+∠CDM=90°,∠DCM+∠BCE=90°,
∴∠CDM=∠BCE,∵∠DMC=∠CBE,
∴△DCM∽△CEB,
∴![]()
∴![]() ,
,
∴y=![]() x+4
x+4
由题意可得![]() ,即
,即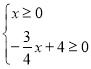
解得:0≤x≤![]()
∴y=![]() x+4(0≤x≤
x+4(0≤x≤![]() )
)
(3)如图3中,
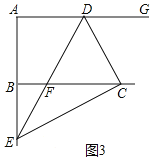
∵CD=CF,
∴∠CDF=∠CFD,
∵AG∥BC,
∴∠CFD=∠ADF,
∴∠EDA=∠EDC,
∵EA⊥DA,EC⊥DC,
∴EA=EC=x+3,
在Rt△BCE中,∵EC2=BE2+BC2,
∴(x+3)2=x2+42,
∴x=![]() ,
,
∴BE=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目