题目内容
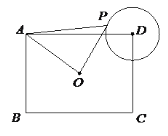
【题目】如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（ ）
A. 4 B. 
C. 
D. 
【答案】D
【解析】解：当P点移动到平行于OA且与⊙D相切时，△AOP面积的最大，如图，∵P是⊙D的切线，∴DP垂直与切线，延长PD交AC于M，则DM⊥AC，∵在矩形ABCD中，AB=3，BC=4，∴AC= 
=5，∴OA= 
，∵∠AMD=∠ADC=90°，∠DAM=∠CAD，∴△ADM∽△ACD，∴
，∵AD=4，CD=3，AC=5，∴DM= 
，∴PM=PD+DM=1+ 
= 
，∴△AOP的最大面积= 
OAPM= 
= 
，故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板：
（1）观察图形，填写下表:
图形 | （1） | （2） | （3） | …… |
黑色瓷砖的块数 | 4 | …… | ||
黑白两种瓷砖的总块数 | 15 | …… |
（2）依上推测，第n个图形中黑色瓷砖的块数为__________________；黑白两种瓷砖的总块数为__________________（都用含n的代数式表示）
（3）白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗？若能，求出是第几个图形；若不能，请说明理由.
