题目内容
【题目】在平面直角坐标系![]() 中,有抛物线
中,有抛物线![]() 和直线
和直线![]() 其中,直线与
其中,直线与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() .将点
.将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
(1)求点![]() 的坐标和抛物线的对称轴;
的坐标和抛物线的对称轴;
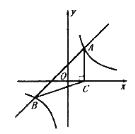
(2)若抛物线与折线段![]() 恰有两个公共点,结合函数图象,求
恰有两个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)C(6,6),对称轴为![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先通过直线![]() 求得A、B坐标,再将点
求得A、B坐标,再将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() 坐标,利用抛物线的对称轴公式求出对称轴即可;
坐标,利用抛物线的对称轴公式求出对称轴即可;
(2)先求出抛物线总会经过的两个定点(4,3),(-1,3),进而可求出抛物线与直线的一个交点坐标(-1,3),再分别讨论当m<0时,及当m>0时,需满足的条件即可.
(1)令![]() 中的y=0,则x=-2,
中的y=0,则x=-2,
令x=0,则y=6
∴A(-2,0),B(0,6),
∵将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
∴C(6,6),
∵抛物线![]() ,
,
∴对称轴为![]()
(2)∵![]()
∴![]()
∴无论m为何值,抛物线总会经过定点(4,3),(-1,3),
又∵当x=-1时,直线y=-3+6=3,
∴直线也经过点(-1,3)
∴无论m为何值,抛物线与直线都总会经过(-1,3),
即(-1,3)为它们的一个交点坐标
当m<0时,如图,
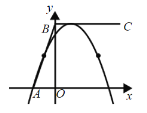
∵抛物线与折线段![]() 恰有两个公共点,
恰有两个公共点,
∴顶点一定在线段BC上,即顶点坐标为(![]() ,6)
,6)
将(![]() ,6)代入
,6)代入![]() 得
得![]() ,
,
此时![]()
令x=-2,则![]() >0,符合题意
>0,符合题意
∴![]() ;
;
当m>0时,如图,
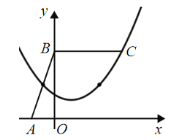
当抛物线经过点C(6,6)时
将(6,6)代入![]() 得
得![]() ,
,
∵抛物线与折线段![]() 恰有两个公共点,
恰有两个公共点,
且抛物线的开口越小,|m|的绝对值越大,
∴![]() .
.
综上所述,![]() 的取值范围为:
的取值范围为: ![]() 或
或![]() .
.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】北京世界园艺博览会(以下简称“世园会”)于2019年4月29日至10月7日在北京市延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的游玩路线,如下表:
A | B | C | D |
漫步世园会 | 爱家乡,爱园艺 | 清新园艺之旅 | 车览之旅 |
小美和小红都计划去世园会游玩,她们各自在这4条路线中任意选择一条,每条线路被选择的可能性相同.
(1)求小美选择路线“清新园艺之旅”的概率是多少?
(2)用画树状图或列表的方法,求小美和小红恰好选择同一条路线的概率.