题目内容
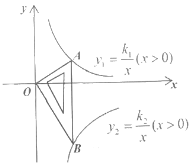
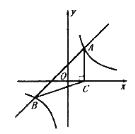
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,
为常数,![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,
两点,![]() 点的坐标为(1,2).
点的坐标为(1,2).
(1)求两个函数的表达式和![]() 点坐标;
点坐标;
(2)过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() ,求
,求![]() 的面积;
的面积;
(3)根据图象直接写出当![]() 时,自变量
时,自变量![]() 的取值范围.
的取值范围.
【答案】(1)一次函数的表达式为![]() ,反比例函数的表达式为
,反比例函数的表达式为![]() ,
,![]() ;(2)3;(3)
;(2)3;(3)![]() 或
或![]() .
.
【解析】
(1)根据待定系数法求出两个函数的表达式,再联立两个表达式可求出![]() 点坐标;
点坐标;
(2)根据点B、C的坐标可得![]() 、点
、点![]() 到
到![]() 的距离为3,再根据三角形的面积公式求解即可;
的距离为3,再根据三角形的面积公式求解即可;
(3)根据两个函数图象的位置,写出自变量![]() 的取值范围即可.
的取值范围即可.
解:(1)∵一次函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]()
解得![]() ,一次函数的表达式为
,一次函数的表达式为![]()
∵反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,
,
∴![]() .
.
∴反比例函数的表达式为![]() .
.
联立方程组
解,得![]() 或
或![]()
∴![]() 点的坐标为
点的坐标为![]()
(2)∵![]() ⊥
⊥![]() 轴,且
轴,且![]() ,
,
∴![]() 点坐标为(1,0).
点坐标为(1,0).
∴![]()
∵![]()
∴点![]() 到
到![]() 的距离为3,
的距离为3,
∴![]() .
.
(3)当一次函数图象在反比例函数图象上方时,![]() 或
或![]() .
.

【题目】某校为了更好地让学生适应中考体育:“1分钟跳绳”项目,对全校九年级200名学生进行了“1分钟跳绳”的测试,现随机抽取20名学生成绩进行分析,过程如下:
收集数据 20名学生的“1分钟跳绳”成绩(单位:个)如下
110 125 134 135 115 146 148 124 153 145
157 160 162 162 165 168 172 128 137 130
整理数据 请你按如下表格分组整理、描述样本数据,并把下列表格补充完整.(说明:每分钟跳绳个数达到160个及以上得满分)
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
人数 |
成绩 |
|
|
等级 |
|
|
人数 |
分析数据 请将下列表格补充完整:
平均数 | 中位数 | 满分率 |
143.8 | 30% |
得出结论
(1)用样本中的统计量估计全校九年级学生“1分钟跳绳”等级为__________;
(2)估计该校九年级200名学生中测试“1分钟跳绳”等级为![]() 的人数.
的人数.
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)