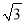题目内容
已知x≠1,(1+x)(1-x)=1- ,(1-x)(1+x+
,(1-x)(1+x+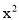 )=1-
)=1-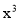 ,(1-x)(1+x+
,(1-x)(1+x+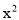 +
+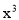 )=1-
)=1-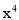 .
.
(1)根据以上式子计算:
①(1-2)×(1+2+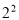 +
+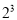 +
+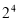 +
+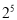 ):②2+
):②2+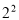 +
+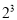 +…+
+…+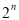 (n为正整数):
(n为正整数):
③(x-1)( 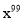 +
+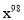 +
+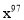 +…+
+…+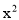 +x+1).
+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=______________:②(a-b) (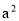 +ab+
+ab+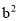 )=_________________:
)=_________________:
③(a-b)( 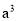 +
+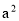 b+
b+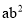 +
+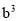 )=_____________.
)=_____________.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


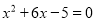 的左边配成完全平方后所得方程为 ( )
的左边配成完全平方后所得方程为 ( )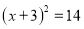 B.
B. 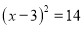 C.
C. 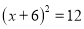 D. 以上答案都不对
D. 以上答案都不对
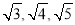 B. 1,
B. 1, 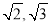
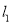 ,
,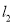 相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D,已知AB=BC=CD=DA=5公里,村庄C到公路
相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D,已知AB=BC=CD=DA=5公里,村庄C到公路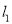 的距离为4公里,则村庄C到公路
的距离为4公里,则村庄C到公路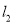 的距离是_____公里.
的距离是_____公里.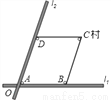
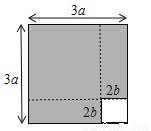
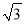 B. 3
B. 3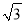 C. 6 D. 6
C. 6 D. 6