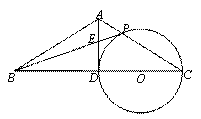
题目内容
定义1:在 中,若顶点
中,若顶点 ,
,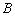 ,
, 按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
 ,
,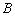 ,
, 按顺时针方向排列,则规定它的面积的相反数为
按顺时针方向排列,则规定它的面积的相反数为 的“有向面积”。“有
的“有向面积”。“有 向面积”用
向面积”用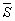 表示,
表示,


 例如图1中,
例如图1中,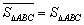 ,图2中,
,图2中,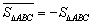 。
。
定义2:在平面内任取一个 和点
和点 (点
(点 不在
不在 的三边所在直线上),称有序数组(
的三边所在直线上),称有序数组( ,
,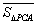 ,
, )为点
)为点 关于
关于 的“
的“ 面积坐标”,记作
面积坐标”,记作 ,例如图3中,菱形
,例如图3中,菱形 的边长为2,
的边长为2,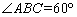 ,则
,则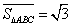 ,点
,点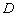 关于
关于 的“面积坐标”
的“面积坐标”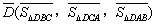 为
为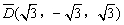 。
。
 在图3中,我们知道
在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为:
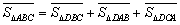 。
。
应用新知:
(1)如图4,正方形 的边长为1,则
的边长为1,则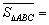 ,点
,点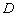 关于
关于 的“面积坐标”是 ;
的“面积坐标”是 ;
探究发现:
(2)在平面直角坐标系 中,点
中,点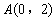 ,
,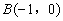 .
.
①若点 是第二象限内任意一点(不在直线
是第二象限内任意一点(不在直线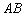 上),设点
上),设点 关于
关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究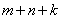 与
与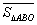 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点
是第四象限内任意一点,请直接写出点 关于
关于 的“面积坐标”(用
的“面积坐标”(用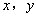 表示);
表示);
解决问题:
(3)在(2)的条件下,点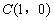 ,
, ,点
,点 在抛物线
在抛物线 上,求当
上,求当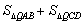 的值最小时,点
的值最小时,点 的横坐标。
的横坐标。
练习册系列答案
相关题目
某市2014年4月份一周空气质量报告中某种污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数和众数分别是( )
A.32,31 B.31,32 C.31,31 D.32,35
如图,在反比例函数 的图象上,有点
的图象上,有点 ,
, ,
, ,
,
 ……
…… (n为正整数,且n≥1),它们的横坐标依次为1,2,3,4……
(n为正整数,且n≥1),它们的横坐标依次为1,2,3,4…… (n为正整数,且n≥1).分别过这些点作
(n为正整数,且n≥1).分别过这些点作
| |
 轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为
轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为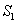 ,
, ,
, ……
…… (n为正整数,且n≥2),那么
(n为正整数,且n≥2),那么 ,
, .(用含有n的代数式表示).
.(用含有n的代数式表示). 




 是以
是以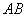 为直径的圆
为直径的圆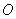 上一点,直线
上一点,直线 与过
与过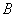 点的切线相交于
点的切线相交于 点
点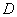 ,点
,点 是
是 的中点,直线
的中点,直线 交直线
交直线 .
. 是⊙O的切线;
是⊙O的切线; (2)若
(2)若 ,
, ,
,
 以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分:
以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分: B.
B. C.
C. D.
D.