题目内容
7.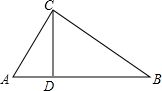 如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}$=$\frac{CD}{BD}$.
如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}$=$\frac{CD}{BD}$.(Ⅰ)求∠ACB的大小;
(Ⅱ)写出图中所有的相似三角形.
分析 (1)由CD是边AB上的高,得到∠ADC=∠CDB=90°,由于$\frac{AD}{CD}$=$\frac{CD}{BD}$,于是得到△ADC∽△CDB,然后根据相似三角形的性质即可得到结论;
(2)根据相似三角形的判定定理即可得到结论.
解答 解:(1)∵CD是边AB上的高,
∴∠ADC=∠CDB=90°,
∵$\frac{AD}{CD}$=$\frac{CD}{BD}$,
∴△ADC∽△CDB,
∴∠A=∠DCB,
∵∠A+∠ACD=90°,
∴∠DCB+∠ACD=90°,
即∠ACB=90°,
(2)由(1)证得∠A=∠BCD,∠ACD=∠B,
∵∠ADC=∠BDC=∠ACB=90°,
∴△ACD∽△BCD,△ACD∽△ABC,△BCD∽△ABC.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
15.函数y=2+$\frac{\sqrt{x+2}}{x+1}$中自变量x的取值范围为( )
| A. | x≥-2 | B. | x≥-2且x≠-1 | C. | x≤-2且x≠-1 | D. | x≤-2 |
2.抛物线y=-$\frac{1}{4}$x2+3的对称轴为( )
| A. | 直线x=3 | B. | 直线x=6 | C. | 直线y=6 | D. | y轴 |
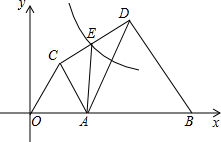 如图,B点的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边△OAC和等边△ABD,连接CD,E为CD的中点,双曲线y=$\frac{k}{x}$(x>0)经过点E,若AE=$\frac{\sqrt{79}}{2}$时,则k=10$\sqrt{3}$或15$\sqrt{3}$.
如图,B点的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边△OAC和等边△ABD,连接CD,E为CD的中点,双曲线y=$\frac{k}{x}$(x>0)经过点E,若AE=$\frac{\sqrt{79}}{2}$时,则k=10$\sqrt{3}$或15$\sqrt{3}$.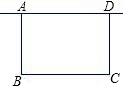 如图,学校准备利用图书馆后面的场地用围栏圈建一个面积为60平方米的长方形ABCD,车棚的一边利用图书馆的后墙,墙长为a.
如图,学校准备利用图书馆后面的场地用围栏圈建一个面积为60平方米的长方形ABCD,车棚的一边利用图书馆的后墙,墙长为a.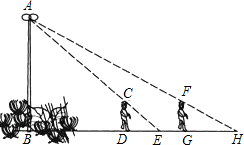 如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.
如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.