题目内容
6.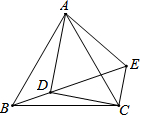 如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
分析 (1)利用旋转的性质和等边三角形的性质先判断出△ADE是等边三角形即可;
(2)利用四边形的内角和即可求出结论;
(3)先求出CD,再用勾股定理即可求出结论.
解答 (1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°-∠ADC-∠AEC-∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC-∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,$DC=\sqrt{D{E^2}-C{E^2}}=\sqrt{{2^2}-{1^2}}=\sqrt{3}$.
点评 此题是旋转的性质,主要考查了等边三角形的性质和判定,勾股定理,解本题的关键是判断出△ADE是等边三角形.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
18.把-(-1),-$\frac{2}{3}$,-|-$\frac{4}{5}$|,0用“>”连起来的式子正确的是( )
| A. | 0>-(-1)>-$\frac{2}{3}$>-|-$\frac{4}{5}$| | B. | -(-1)>0>-|-$\frac{4}{5}$|>-$\frac{2}{3}$ | C. | 0>-$\frac{2}{3}$>-|-$\frac{4}{5}$|-(-1) | D. | -(-1)>0>-$\frac{2}{3}$>-|-$\frac{4}{5}$| |
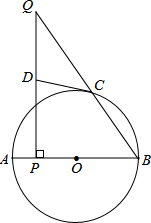 如图所示,AB为⊙O的直径,点C在⊙O上,P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q
如图所示,AB为⊙O的直径,点C在⊙O上,P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,则∠ACA′的度数是50°.
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,则∠ACA′的度数是50°. 如图,画出△ABC关于点O中心对称的△A′B′C′.(不写画法,请保留作图痕迹)
如图,画出△ABC关于点O中心对称的△A′B′C′.(不写画法,请保留作图痕迹)