题目内容
如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.


证明:连接OP、OQ,分别交AB.CD于点M、N,再连接OA、OD、MN,并延长OK交PQ于中
∵PA、PB切⊙O于点A、B
∴OA⊥PA,OP⊥AB
∴OA2=OM?OP
同理OD2=ON?OQ
∵OA=OD∴OM?OP=ON?OQ
∴∠OMN=∠OQP
∵∠OMB=∠ONK=96°
∴∠OMB+∠ONK=196°
∴∠OMN=∠OKN∠OKN=∠OQP,
∴∠OMN=∠OKN∠OKN=∠O中Q=96°
∴O中⊥PQ
即OK⊥PQ

练习册系列答案
相关题目
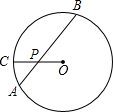 如图,⊙O的弦AB平分半径OC,交OC于P点,已知PA和PB的长分别是方程x2-12x+24=0的两根,则此圆的直径为( )
如图,⊙O的弦AB平分半径OC,交OC于P点,已知PA和PB的长分别是方程x2-12x+24=0的两根,则此圆的直径为( )A、8
| ||
B、6
| ||
C、4
| ||
D、2
|
 13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ. 如图,⊙O′的弦AB是⊙O的直径,点O′在⊙O上,设图中两个阴影部分的面积分别为S和S′,则S′:S=
如图,⊙O′的弦AB是⊙O的直径,点O′在⊙O上,设图中两个阴影部分的面积分别为S和S′,则S′:S= 如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.