题目内容
 如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
 证明:连接OP、OQ,分别交AB.CD于点M、N,再连接OA、OD、MN,并延长OK交PQ于H
证明:连接OP、OQ,分别交AB.CD于点M、N,再连接OA、OD、MN,并延长OK交PQ于H∵PA、PB切⊙O于点A、B
∴OA⊥PA,OP⊥AB
∴OA2=OM•OP
同理OD2=ON•OQ
∵OA=OD∴OM•OP=ON•OQ
∴∠OMN=∠OQP
∵∠OMB=∠ONK=90°
∴∠OMB+∠ONK=180°
∴∠OMN=∠OKN∠OKN=∠OQP,
∴∠OMN=∠OKN∠OKN=∠OHQ=90°
∴OH⊥PQ
即OK⊥PQ
分析:此题关键是作出辅助线,证明OK⊥PQ,所以首先延长OK交PQ于H,其余几条都是常用辅助线,再利用四点共圆可以解决.
点评:此题主要考查了四点共圆的判定方法,以及常用辅助线的作法,综合性比较强.

练习册系列答案
相关题目
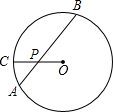 如图,⊙O的弦AB平分半径OC,交OC于P点,已知PA和PB的长分别是方程x2-12x+24=0的两根,则此圆的直径为( )
如图,⊙O的弦AB平分半径OC,交OC于P点,已知PA和PB的长分别是方程x2-12x+24=0的两根,则此圆的直径为( )A、8
| ||
B、6
| ||
C、4
| ||
D、2
|
 13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ. 如图,⊙O′的弦AB是⊙O的直径,点O′在⊙O上,设图中两个阴影部分的面积分别为S和S′,则S′:S=
如图,⊙O′的弦AB是⊙O的直径,点O′在⊙O上,设图中两个阴影部分的面积分别为S和S′,则S′:S=