题目内容
2.k取何非负整数时,代数式$\frac{2k-1}{2}$-$\frac{2k+5}{3}$的值不小于代数式$\frac{6k-7}{4}$-1的值.分析 根据题意列不等式$\frac{2k-1}{2}$-$\frac{2k+5}{3}$≥$\frac{6k-7}{4}$-1,然后通过去分母、去括号、移项、合并得到x≤$\frac{1}{2}$,再在此范围内找出非负整数即可得到k的值.
解答 解:根据题意得$\frac{2k-1}{2}$-$\frac{2k+5}{3}$≥$\frac{6k-7}{4}$-1,
去分母得6(2k-1)-4(2k+5)≥3(6k-7)-12,
去括号得12k-6-8k-20≥18k-21-12,
移项得12k-8k-18k≥-21-12+6+20,
合并得-14k≥-7,
系数化为1得x≤$\frac{1}{2}$,
而k为非负整数,
所以k=0.
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
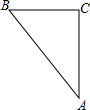 如图,小明和小方分别在C处同时出发,小明以每小时40千米的速度向南走,小方以每小时30千米的速度向西走,2小时后,小明在A处,小方在B处,请求出AB的距离.
如图,小明和小方分别在C处同时出发,小明以每小时40千米的速度向南走,小方以每小时30千米的速度向西走,2小时后,小明在A处,小方在B处,请求出AB的距离.