题目内容
 如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)通过作辅助线证明三角形全等,得出对应边相等,在△CFG中,根据三边关系得出结论;
(2)根据(1)的结论,证出平行线,得出∠ACG=90°,再根据勾股定理即可得出结论.
(2)根据(1)的结论,证出平行线,得出∠ACG=90°,再根据勾股定理即可得出结论.
解答:(1)延长ED至G,使DG=DE,连接CG、FG,如图所示:
在△CDG和△BDE中,
∴△CDG≌△BDE(SAS),
∴CG=BE,
∵DE⊥DF,DG=DE,
∴EF=FG,
在△CFG中,CG+CF>FG,
∴BE+CF>EF;
(2)当∠A=90°时,BE2+CF2=EF2;
由(1)得,△CDG≌△BDE,
∴∠DCG=∠DBE,
∴AB∥CG,∵∠A=90°,
∴∠ACG=90°,
在Rt△CFG中,由•勾股定理得,CG2+CF2=FG2,
由(1)知,BE=CG,EF=FG,
∴BE2+CF2=EF2.

在△CDG和△BDE中,
|
∴△CDG≌△BDE(SAS),
∴CG=BE,
∵DE⊥DF,DG=DE,
∴EF=FG,
在△CFG中,CG+CF>FG,
∴BE+CF>EF;
(2)当∠A=90°时,BE2+CF2=EF2;
由(1)得,△CDG≌△BDE,
∴∠DCG=∠DBE,
∴AB∥CG,∵∠A=90°,
∴∠ACG=90°,
在Rt△CFG中,由•勾股定理得,CG2+CF2=FG2,
由(1)知,BE=CG,EF=FG,
∴BE2+CF2=EF2.
点评:考查了全等三角形的判定与性质,通过作辅助线证明三角形全等,得出相等的边和角,证出结论;构造三角形全等是解决问题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
下列说法正确的是( )
| A、a5-a4bc是五次多项式 |
| B、-1是单项式 |
| C、3(x+y)是单项式 |
| D、单项式2π的系数是2 |
2014年11月7日,北京市民迎来了6天的APEC假期.当天,北京青年报记者从北京铁路局 获悉,从11月6日开始,各火车站的出京客流就迎来了小高峰,出京客流超过410 000人.将410 000用科学记数法表示,结果正确的是( )
| A、41×104 |
| B、4.1×105 |
| C、4.1×104 |
| D、4.1×106 |
据深圳市统计局统计数据显示,2014年10月深圳市“新能源产业增加值”为34亿元,数据34亿元用科学记数法表示为( )
| A、3.4×109元 |
| B、3.4×108元 |
| C、0.34×109元 |
| D、34×108元 |
如图是一中国象棋棋盘,右侧是一颗反面朝上的棋子,这个棋子的俯视图是( )

A、 |
B、 |
C、 |
D、 |
 如图,直线AB与CD相交于点O,射线OE平分∠BOF.
如图,直线AB与CD相交于点O,射线OE平分∠BOF.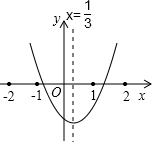 如图,二次函数y=ax2+bx+c图象的对称轴是x=
如图,二次函数y=ax2+bx+c图象的对称轴是x=