题目内容
 如图,直线AB与CD相交于点O,射线OE平分∠BOF.
如图,直线AB与CD相交于点O,射线OE平分∠BOF.(1)∠AOD的对顶角是
(2)若∠AOD=20°,∠DOF:∠FOB=1:7,求∠EOC的度数.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)根据对顶角和邻补角的定义可直接得出答案;
(2)根据∠AOD=20°和∠DOF:∠FOB=1:7,求出∠BOF等于140°,所以∠EOB等于70°,所以∠EOC等于90°.
(2)根据∠AOD=20°和∠DOF:∠FOB=1:7,求出∠BOF等于140°,所以∠EOB等于70°,所以∠EOC等于90°.
解答:解:(1)∵直线AB与CD相交于点O,
∴∠AOD的对顶角是∠BOC,∠BOC的邻补角是∠AOC,∠BOD;
(2)∵OE平分∠BOF,
∴∠BOE=EOF,
∵∠DOF:∠FOB=1:7,∠AOD=20°,
∴∠DOF=
∠BOD=
×(180°-20°)=20°,
∴∠BOF=140°,
∴∠BOE=
∠BOE=
∠BOF=
×140°=70°,
∴∠EOC=∠BOC+∠EOB=70°+20°=90°;
所以∠EOC等于90°.
∴∠AOD的对顶角是∠BOC,∠BOC的邻补角是∠AOC,∠BOD;
(2)∵OE平分∠BOF,
∴∠BOE=EOF,
∵∠DOF:∠FOB=1:7,∠AOD=20°,
∴∠DOF=
| 1 |
| 8 |
| 1 |
| 8 |
∴∠BOF=140°,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOC=∠BOC+∠EOB=70°+20°=90°;
所以∠EOC等于90°.
点评:本题考查了对顶角、邻补角以及角平分线的性质,主要利用对顶角相等,邻补角的定义和角平分线的定义求解.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
2014年7月郑州晚报报道省政府下发《河南省科学推进新型城镇化三年行动计划》,到2016年,郑州中心城区常住人口达到600.2万人以上,此数用科学记数法表示正确的是( )
| A、60.02×105 |
| B、6.002×106 |
| C、6.002×102 |
| D、6.002×107 |
 如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
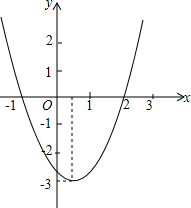 二次函数y=ax2+bx+c(a≠0)的图象如图,根据图象回答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图,根据图象回答下列问题: 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,已知AF=1,DF=DC=2,则BD=
如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,已知AF=1,DF=DC=2,则BD=