题目内容
 两个同心圆的半径之比为3:5,AB是大圆的直径,大圆的弦BC与小圆相切,若AC=12,那么BC=
两个同心圆的半径之比为3:5,AB是大圆的直径,大圆的弦BC与小圆相切,若AC=12,那么BC=
- A.6
- B.8
- C.10
- D.16
D
分析:设弦BC与小圆相切于点D,连接OD,OD⊥BC,AB为大圆的直径,AC⊥BC,故OD为△ABC的中位线;因由已知可知AC=12,OD即可知,两个同心圆的半径之比为3:5,可求得大圆半径,再由勾股定理可求得BC的长.
解答: 解:设弦BC与小圆相切于点D,连接OD,如下图所示:
解:设弦BC与小圆相切于点D,连接OD,如下图所示:
∵AB为大圆的直径,
∴AC⊥BC,
∵OD⊥BC,O为AB的中点∴OD∥AC
∴OD为△ABC的中位线;
∵AC=12,
∴OD=6;
∵两个同心圆的半径之比为3:5,
∴大圆半径为10,
∴AB=20,
∴BC= =16.
=16.
故选D.
点评:本题主要考查了切线的性质及勾股定理的应用.
分析:设弦BC与小圆相切于点D,连接OD,OD⊥BC,AB为大圆的直径,AC⊥BC,故OD为△ABC的中位线;因由已知可知AC=12,OD即可知,两个同心圆的半径之比为3:5,可求得大圆半径,再由勾股定理可求得BC的长.
解答:
 解:设弦BC与小圆相切于点D,连接OD,如下图所示:
解:设弦BC与小圆相切于点D,连接OD,如下图所示:∵AB为大圆的直径,
∴AC⊥BC,
∵OD⊥BC,O为AB的中点∴OD∥AC
∴OD为△ABC的中位线;
∵AC=12,
∴OD=6;
∵两个同心圆的半径之比为3:5,
∴大圆半径为10,
∴AB=20,
∴BC=
 =16.
=16.故选D.
点评:本题主要考查了切线的性质及勾股定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
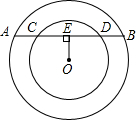 如图,两个同心圆中,大圆的弦AB交小圆与点C、D,OE⊥AB垂足为E,且OE=1,若AB=4,CD=2,则两个同心圆的半径之比为( )
如图,两个同心圆中,大圆的弦AB交小圆与点C、D,OE⊥AB垂足为E,且OE=1,若AB=4,CD=2,则两个同心圆的半径之比为( )| A、3:2 | ||||
B、
| ||||
C、
| ||||
| D、2:1 |
 如图,同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )
如图,同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )| A、3:2 | ||||
B、
| ||||
C、
| ||||
| D、5:4 |
 两个同心圆的半径之比为3:5,AB是大圆的直径,大圆的弦BC与小圆相切,若AC=12,那么BC=( )
两个同心圆的半径之比为3:5,AB是大圆的直径,大圆的弦BC与小圆相切,若AC=12,那么BC=( )| A、6 | B、8 | C、10 | D、16 |

 :2
:2 :
:
