题目内容
 已知,如图,AB∥CD,直线a交AB、CD分别于点E、F,点M在线段EF上,P是直线CD上的一个动点,(点P不与F重合)
已知,如图,AB∥CD,直线a交AB、CD分别于点E、F,点M在线段EF上,P是直线CD上的一个动点,(点P不与F重合)(1)当点P在射线FC上移动时,∠FMP、∠FPM和∠AEF之间的数量关系是:
(2)当点P在射线FD上移动时,∠FMP、∠FPM和∠AEF之间的数量关系是:
考点:平行线的性质
专题:
分析:(1)根据平行线的性质可得∠EFD=∠AEF,然后在△MFP中,利用三角形的外角的性质即可求解;
(2)根据平行线的性质可得∠EFD=∠AEF,然后在△MFP中,利用三角形的内角和定理即可求解.
(2)根据平行线的性质可得∠EFD=∠AEF,然后在△MFP中,利用三角形的内角和定理即可求解.
解答:解:(1)∵AB∥CD,
∴∠EFD=∠AEF,
又∵∠EFD=∠FMP+∠FPM,
∴∠AEF=∠FMP+∠FPM;
(2)当点P在射线FD上移动时,如右图:
∵AB∥CD,
∴∠EFD=∠AEF,
又∵∠FMP+∠FPM+∠EFD=180°,
∴∠FMP+∠FPM+∠AEF=180°.
故答案是:∠AEF=∠FMP+∠FPM,
∠FMP+∠FPM+∠AEF=180°.
∴∠EFD=∠AEF,
又∵∠EFD=∠FMP+∠FPM,
∴∠AEF=∠FMP+∠FPM;
(2)当点P在射线FD上移动时,如右图:

∵AB∥CD,
∴∠EFD=∠AEF,
又∵∠FMP+∠FPM+∠EFD=180°,
∴∠FMP+∠FPM+∠AEF=180°.
故答案是:∠AEF=∠FMP+∠FPM,
∠FMP+∠FPM+∠AEF=180°.
点评:本题比较简单,考查的是平行线的性质及三角形内角与外角的关系.

练习册系列答案
相关题目
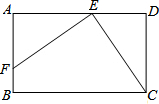 如图,在矩形ABCD中,E为AD上的一点,EF⊥CE交AB于F,且CE=EF,
如图,在矩形ABCD中,E为AD上的一点,EF⊥CE交AB于F,且CE=EF, 如图,已知∠1+∠2=180°,∠B=∠3,求证:DE∥BC.
如图,已知∠1+∠2=180°,∠B=∠3,求证:DE∥BC. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,CD=2cm,则BD的长是
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,CD=2cm,则BD的长是