Question

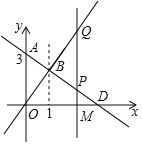
【题目】如图，A点的纵坐标为3，过A点的一次函数图象与正比例函数y＝2x的图象相交于点B．

（1）求该一次函数的表达式；

（2）若点P为第一象限内直线AB上的一动点，设点P的横坐标为m，过点P作x轴的垂线交正比例函数图象于点Q，交x轴于点M．

①当△AOB≌△PQB时，求线段PM的长．

②当线段PQ＝AO时，请直接写出点P的坐标．

Answer 1

【答案】（1）y＝﹣x+3；（2）①1；②点P的坐标为(，)或(，)．

【解析】

（1）根据图象上点的坐标特征求得B的坐标，然后根据待定系数法即可求得一次函数的解析式；

（2）①根据题意P（m，﹣m+3），则Q（m，2m），即可得到PQ＝|2m﹣（﹣m+3）|＝|3m﹣3|，当△AOB≌△PQB时，AO＝PQ，即|3m﹣3|＝3，然后结合题意即可求得P（2，1），PM＝1；

②根据题意得到|3m﹣3|＝，求得m的值，从而求得P的坐标．

解：（1）∵点B的横坐标为1，且点B在正比例函数y＝2x的图象上，

∴y＝2×1＝2，

∴B（1，2），

∵A点的纵坐标为3，

设一次函数的解析式为y＝kx+3，

代入B（1，2）得，2＝k+3，

解得k＝﹣1，

∴一次函数的解析式为y＝﹣x+3；

（2）①∵点P为第一象限内直线AB上的一动点，且点P的横坐标为m，

∴P（m，﹣m+3），

∵PQ⊥x轴，且Q在y＝2x的图象上，

∴Q（m，2m），

∴PQ＝|2m﹣（﹣m+3）|＝|3m﹣3|，

当△AOB≌△PQB时，

∴AO＝PQ，即|3m﹣3|＝3，

∴m＝2或0（由点P在第一象限，故舍去），

∴P（2，1），PM＝1；

②当线段PQ＝AO时，则|3m﹣3|＝，

当3m﹣3＝时，

解得m＝，

此时P（，）；

当﹣3m+3＝时，

解得m＝，

此时P（，）．

综上：点P的坐标为(，)或(，)．