题目内容
【题目】商店销售某上市新品,期间共销售该产品![]() 天,设销售时间为
天,设销售时间为![]() 天,第一天销售单价定为
天,第一天销售单价定为![]() 元/千克,售出
元/千克,售出![]() 千克.从第
千克.从第![]() 天至第
天至第![]() 天,该产品成本价为
天,该产品成本价为![]() 元/千克,销售单价每天降低
元/千克,销售单价每天降低![]() 元,销售量每天增加
元,销售量每天增加![]() 千克.从第
千克.从第![]() 天开始,成本价降为
天开始,成本价降为![]() 元/千克,销售单价稳定在
元/千克,销售单价稳定在![]() 元/千克,每天销售量
元/千克,每天销售量![]() (千克)与第
(千克)与第![]() 天满足一次函数关系
天满足一次函数关系![]() ,设第
,设第![]() 天销售利润为
天销售利润为![]() 元
元
![]() 直接写出
直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 问销售该商品第几天时,当天销售利润最大,最大利润是多少?
问销售该商品第几天时,当天销售利润最大,最大利润是多少?
![]() 该商品在这
该商品在这![]() 天的销售过程中,共有多少天每天销售利润不低于
天的销售过程中,共有多少天每天销售利润不低于![]() 元?
元?
【答案】(1)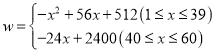 ;(2)销售该商品第
;(2)销售该商品第![]() 天时,当天销售利润最大,最大利润是
天时,当天销售利润最大,最大利润是![]() 元;(3)当有
元;(3)当有![]() 天,每天销售利润不低
天,每天销售利润不低![]() 元
元
【解析】
(1)需要分情况讨论,第一阶段时间在![]() ,第二阶段
,第二阶段![]() ,根据题意列式化简即可;
,根据题意列式化简即可;
(2)分别计算第一阶段,第二阶段的最大利润,两者相比较,最大的即作为最大利润;
(3)分别计算第一阶段,第二阶段利润不低于1232元的天数,两者相加即可.
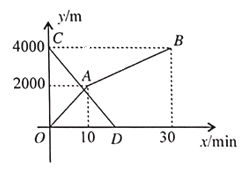
解:(1)由题意可得,可列方程,
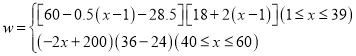
整理得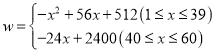
(2)由(1)得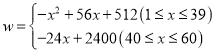
![]() 当
当![]() 时,
时,![]()
![]()
![]() 时,有最大值
时,有最大值
即当![]() 时,最大利润为
时,最大利润为![]() 元
元
当![]() 时,
时,![]()
![]()
![]() 随着
随着![]() 的增大而减少
的增大而减少
![]() 时有最大值
时有最大值
即![]()
综上所述,销售该商品第![]() 天时,当天销售利润最大,最大利润是
天时,当天销售利润最大,最大利润是![]() 元.
元.
![]() 当
当![]() 时,
时,![]()
得![]()
![]() 为整数
为整数
![]()
共计9天
![]() 当
当![]() 时,有
时,有![]()
解得![]()
![]() 时,
时,![]()
共计17天
∵![]()
故有![]() 天,每天销售利润不低
天,每天销售利润不低![]() 于元
于元

【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
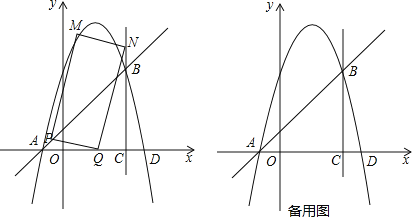
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
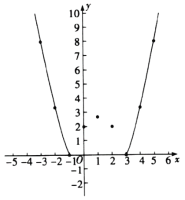
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程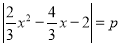 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.