题目内容
20.如图,已知AB∥CD,直线l分别截AB、CD于E、C两点,M是线段EC上一动点(不与E、C重合),过M点作MN⊥CD于点N,连结EN.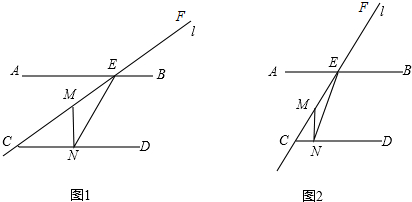
(1)如图1,当∠ECD=40°时,填空:∠FEB=40°;∠MEN+∠MNE=50°;
(2)如图2,当∠ECD=α°时,猜想∠MEN+∠MNE的度数与α的关系,并证明你的结论.
分析 (1)直接根据平行线的性质可得出∠FEB的度数,再由MN⊥CD,由三角形内角和定理可求出∠CMN的度数,根据三角形外角的性质即可得出结论;
(2)根据AB∥CD,∠ECD=α°可得出∠AEC=∠ECD=α°且∠AEN+∠CNE=180°,由MN⊥CD得出∠MNC=90°,根据三角形内角和定理即可得出结论.
解答 解:(1)∵AB∥CD,∠ECD=40°,
∴∠FEB=∠ECD=40°;
∵MN⊥CD,
∴∠CNM=90°,
∴∠CMN=90°-∠ECN=90°-40°=50°.
∵∠CMN是△EMN的外角,
∴∠CMN=∠MEN+∠MNE=50°.
故答案为:40°,50°;
(2)猜想:∠MEN+∠MNE=90°-α°.
证明如下:∵AB∥CD,∠ECD=α°
∴∠AEC=∠ECD=α°且∠AEN+∠CNE=180°.
又∵MN⊥CD
∴∠MNC=90°,
∴90°+∠MEN+∠MNE+α°=180°,
∴∠MNE+∠MEN=90°-α°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
11.某市“五一”期间13条高速公路免费放行247万辆车次,免费余额预计达到4960万元,将4960万元用科学记数法表示为( )元.
| A. | 4.96×105 | B. | 4.96×104 | C. | 4.96×106 | D. | 4.96×107 |
15.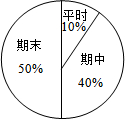 小军和小明八年级上学期的数学成绩如下表所示:
小军和小明八年级上学期的数学成绩如下表所示:
(1)计算小军和小明上学期平时的平均成绩;
(2)如果总评成绩按扇形图所示的权重计算,问小军和小明谁的上学期总评成绩高?
 小军和小明八年级上学期的数学成绩如下表所示:
小军和小明八年级上学期的数学成绩如下表所示:| 测验 类别 | 平 时 | 期中 考试 | 期末 考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 小军成绩 | 110 | 105 | 95 | 110 | 108 | 112 |
| 小明成绩 | 105 | 95 | 100 | 115 | 115 | 95 |
(2)如果总评成绩按扇形图所示的权重计算,问小军和小明谁的上学期总评成绩高?
5.对于函数y=f(x),有以下说法:
①y是x的函数;②对于不同的x,y的值也不同;③f(a)表示当x=a时,函数f(x)的值,它是一个常量;④f(x)一定可以用一个具体的式子表示出来,其中正确的说法的个数是( )
①y是x的函数;②对于不同的x,y的值也不同;③f(a)表示当x=a时,函数f(x)的值,它是一个常量;④f(x)一定可以用一个具体的式子表示出来,其中正确的说法的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.下列约分正确的是( )
| A. | $\frac{x+y}{{x}^{2}+xy}$=$\frac{1}{x}$ | B. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | C. | $\frac{x+y}{x+y}=0$ | D. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ |
 如图,∠B=80°,∠C=50°,AD是△ABC的高,AE是∠CAB的平分线,求∠DAE.
如图,∠B=80°,∠C=50°,AD是△ABC的高,AE是∠CAB的平分线,求∠DAE. 如图所示是长方形鸡场的平面示意图,场的长度为19米,一边靠墙,另外三边长用铁丝网围成,且铁路总长度为36米,若所围成的面积为160平方米,求长方形鸡场的长和宽.
如图所示是长方形鸡场的平面示意图,场的长度为19米,一边靠墙,另外三边长用铁丝网围成,且铁路总长度为36米,若所围成的面积为160平方米,求长方形鸡场的长和宽. 如图,点P是正方形ABCD对角线BD上的一点,PM⊥BC,PN⊥DC,垂足分别为M、N.
如图,点P是正方形ABCD对角线BD上的一点,PM⊥BC,PN⊥DC,垂足分别为M、N. 小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是58度.
小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是58度.