题目内容
一元二次方程ax2+bx+c=0（a≠0）只有一个根是0的条件是（ ）A．b=0，c=0
B．c=0
C．c=0，b≠0
D．b=0，c≠0
【答案】分析：由题意可知：根据根与系数的关系可以用a、b、c三个字母来表示两根的和与积，再根据只有一根为0即可求得符合题意的条件．
解答：解：根据根与系数的关系与一元二次方程ax2+bx+c=0（a≠0）只有一个根是0可得：
x1+x2=-
≠0，
x1•x2=
=0；
∴c=0，b≠0；
故答案为C．
点评：本题考查的是一元二次方程的根即方程的解的定义和一元二次方程根与系数的关系，要求灵活运用根与系数关系求解．
解答：解：根据根与系数的关系与一元二次方程ax2+bx+c=0（a≠0）只有一个根是0可得：
x1+x2=-
≠0，x1•x2=
=0；∴c=0，b≠0；
故答案为C．
点评：本题考查的是一元二次方程的根即方程的解的定义和一元二次方程根与系数的关系，要求灵活运用根与系数关系求解．
练习册系列答案
应用题作业本系列答案
相关题目
一元二次方程ax2+bx+c=0（a≠0，b2-4ac≥0）的两实根之和（ ）
| A、与c无关 | B、与b无关 | C、与a无关 | D、与a，b，c都有关 |
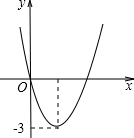（2012•泰安）二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）