题目内容
2. 已知:如图,正方形ABCD中,点E,M,N分别在AB,BC,AD边上,CE=MN,求证:CE⊥MN.
已知:如图,正方形ABCD中,点E,M,N分别在AB,BC,AD边上,CE=MN,求证:CE⊥MN.
分析 作NF⊥BC于F,先根据HL证明Rt△BCE≌Rt△NFM,得出对应角相等,再根据角的互余关系,即可得出结论.
解答 证明:作NF⊥BC于F,如图所示: 则∠NFM=90°,四边形CDNF是矩形,
则∠NFM=90°,四边形CDNF是矩形,
∴NF=CD,
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=90°,
∴BC=NF,
在Rt△BCE和Rt△NFM中,$\left\{\begin{array}{l}{CE=MN}\\{BC=NF}\\{\;}\end{array}\right.$,
∴Rt△BCE≌Rt△NFM(HL),
∴∠1=∠2,
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠4=90°,
∴CE⊥MN.
点评 本题考查了正方形的性质以及全等三角形的判定与性质;通过作辅助线构造三角形全等是解决问题的关键.

练习册系列答案
相关题目
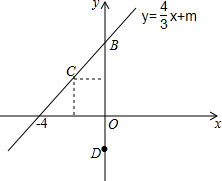 如图,已知一次函数y=$\frac{4}{3}$x+m的图象与x轴交于A(-6,0),交y轴于点B.
如图,已知一次函数y=$\frac{4}{3}$x+m的图象与x轴交于A(-6,0),交y轴于点B.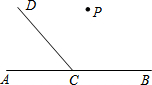 按照要求画图
按照要求画图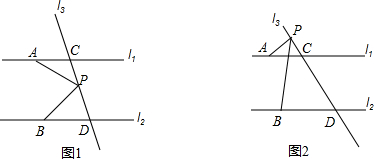
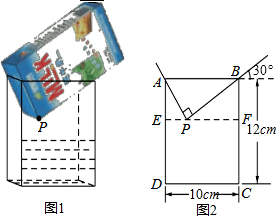 将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题:
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题: 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论: