题目内容
1．已知在六边形ABCDEF中，边AB的长为（a+2b）厘米，边BC比AB短（a-b）厘米，边CD比BC长（2a-3b）厘米，边DE的长为BC与CD两条边长的和，边EF的长为（a+b）厘米．（1）用含a，b的式子表示DE的长；
（2）若AF的长为（3a-2b）厘米，当a=4，b=2时，求六边形ABCDEF的周长．
分析 （1）根据边DE的长为BC与CD两条边长的和列式计算即可；
（2）根据六边形ABCDEF的周长的定义，将6条边相加，化为最简形式，再将a=4，b=2代入计算即可．
解答 解：（1）∵BC的长为（a+2b）-（a-b）=a+2b-a+b=3b，
边CD的长为（2a-3b）+3b=2a，
∴边DE的长为（2a+3b）厘米；
（2）六边形ABCDEF的周长为（a+2b）+3b+2a+（2a+3b）+（a+b）+（3a-2b）
=a+2b+3b+2a+2a+3b+a+b+3a-2b
=9a+7b，
当a=4，b=2时，原式=9×4+7×2=50（厘米）．
点评 本题考查了整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．根据题意列出式子是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3．下列方程中，是一元二次方程的是（ ）
| A． | x-y2=1 | B． | $\sqrt{{x}^{2}-1}$=0 | C． | $\frac{1}{{x}^{2}}$-1=0 | D． | $\frac{{x}^{2}}{2}$+$\frac{x}{3}$-1=0 |
7．如果一个角的补角是150°，那么这个角的度数是（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 120° |
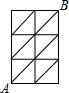如图，在6个边长都为1的小正方形及其部分对角线构成的图形中，从点A到点B只能沿图中的线段走，那么从点A到点B的最短的走法共有（ ）