题目内容
12.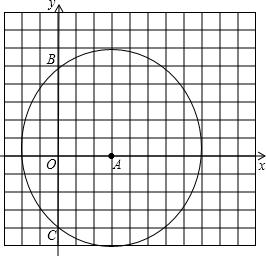 如图所示,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系.圆心为A(3,0)的A被y轴截得的弦长BC=8.解答下列问题:
如图所示,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系.圆心为A(3,0)的A被y轴截得的弦长BC=8.解答下列问题:(1)⊙A的半径为5;
(2)若将⊙A先向上平移2个单位,再向右平移3个单位得到⊙D,则⊙D的圆心D点的坐标是(6,2);⊙D与x轴的位置关系是相交;⊙D与y轴的位置关系是相离;
(3)若将⊙A沿着水平方向平移2或8个单位长度,⊙A即可与y轴相切.
分析 (1)由垂径定理和勾股定理求出AB即可;
(2)由平移的性质得出⊙D的圆心D点的坐标,得出D到x轴的距离为2,到y轴的距离为6,2<5<6,即可得出⊙D与x轴、y轴的位置关系;
(3)由平移的性质和d=r时直线与圆相切即可得出结果.
解答 解:(1)由垂径定理得:OB=$\frac{1}{2}$BC=4,∵A(3,0),
∴OA=3,
由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
即⊙A的半径为5;
故答案为:5;
(2)根据题意得:⊙D的圆心D点的坐标是(6,2);
∵D到x轴的距离为2,到y轴的距离为6,
⊙D的半径=5,2<5<6,
∴⊙D与x轴相交,与y轴相离;
故答案为:(6,2),相交,相离;
(3)∵A(3,0),⊙A的半径为5,
当圆心A到y轴的距离=5时,
即⊙A沿着水平方向向右平移2高或向左平移8个单位长度,
∴⊙A即可与y轴相切.
故答案为:2或8.
点评 本题考查了勾股定理、直线与圆的位置关系、坐标与图形性质、平移的性质;熟练掌握平移的性质,由勾股定理求出半径是解决问题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
17.在-2,3,-(-0.75),-5,7,-3,0,4各数中,负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.下列四组线段中,可构成直角三角形的是( )
| A. | 1.5,2,2.5 | B. | 1,2,3 | C. | 1,$\sqrt{2}$,3 | D. | 2,3,4 |



