题目内容
14.已知:△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120°等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60°.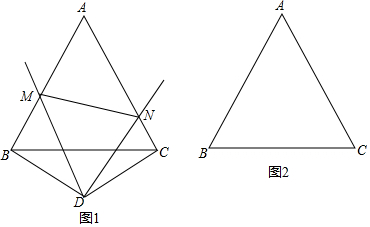
(1)如图1,当点D在△ABC外部时,求证:BM+CN=MN;
(2)在(1)的条件下求△AMN的周长;
(3)当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.
分析 (1)延长AB至F,使BF=CN,连接DF,只要证明△BDF≌△CND,△DMN≌△DMF即可解决问题;
(2)利用(1)中结论即可解决问题;
(3)延长BD交AC于P,CD于Q,令KP=QM,交AC于P,连接DK.通过证明△BDQ≌△CDP,△MDQ≌△PDK,△MDN≌△KDN证得△AMN的周长=$\frac{1}{2}$(AB+AC)=3.
解答 解:(1)延长AB至F,使BF=CN,连接DF,
∵△BDC是等腰三角形,且∠BDC=120°
∴∠BCD=∠DBC=30°
∵△ABC是边长为3的等边三角形
∴∠ABC=∠BAC=∠BCA=60°
∴∠DBA=∠DCA=90°
在Rt△BDF和Rt△CND中,
∵BF=CN,DB=DC
∴△BDF≌△CND
∴∠BDF=∠CDN,DF=DN
∵∠MDN=60°
∴∠BDM+∠CDN=60°
∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边
∴△DMN≌△DMF,
∴MN=MF,
∵MF=BM+BF=MN+CN,
∴MN=BM+CN.
(2)∵MN=BM+CN,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.
(3)延长BD交AC于P,CD于Q,令KP=QM,交AC于P,连接DK.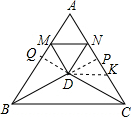
∵△BDC是等腰三角形,且∠BDC=120°
∴BD=CD,∠DBC=∠DCB=30°,∠BDQ=∠CDP=60°
又∵△ABC等边三角形
∴∠ABC=∠ACB=60°
∴∠MBD=∠PCD=30°,CQ⊥AB,BP⊥AC,
∴AQ=BQ=$\frac{1}{2}$AB=$\frac{3}{2}$,AP=PC=$\frac{1}{2}$AC=$\frac{3}{2}$,
在△BDQ和△CDP中,
$\left\{\begin{array}{l}{∠QBD=∠PCD}\\{BD=CD}\\{∠BDQ=∠CDP}\end{array}\right.$,
∴△BDQ≌△CDP(ASA),
∴BQ=PC,QD=PD,
∵CQ⊥AB,BP⊥AC,
∴∠MQD=∠DPK=90°,
在△MDQ与△PDK中,
$\left\{\begin{array}{l}{QD=PD}\\{∠MQD=∠DPK}\\{QM=PK}\end{array}\right.$,
∴△MDQ≌△PDK(SAS),
∴∠QDM=∠PDK,DM=DK,
∵∠BDQ=60°∠MDN=60°,
∴∠QDM+∠PDN=60°,
∴∠PDK+∠PDN=60°,
即∠KDN=60°,
在△MDN与△KDN中,
$\left\{\begin{array}{l}{DM=DK}\\{∠MDN=∠KDN=60°}\\{DN=DN}\end{array}\right.$,
∴△MDN≌△KDN(SAS),
∴MN=KN=NP+PK,
∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AQ+AP=$\frac{3}{2}$+$\frac{3}{2}$=3
故△AMN的周长为3.
点评 本题考查等边三角形的性质、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.

 如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )
如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )| A. | 18x+15x-x2=$\frac{1}{3}$×15×18 | B. | (18-x)(15-x)=$\frac{1}{3}$×15×18 | ||
| C. | 18x+15x=$\frac{1}{3}$×15×18 | D. | 18x+15x+x2=$\frac{1}{3}$×15×18 |
 如图,关于线段、射线、直线的条数,说法正确的是( )
如图,关于线段、射线、直线的条数,说法正确的是( )| A. | 五条线段,三条射线 | B. | 一条射线,三条线段 | ||
| C. | 三条线段,三条射线 | D. | 三条线段,两条射线,一条直线 |
| A. | y1=y2 | B. | y1<y2 | C. | y1>y2 | D. | 不能确定 |
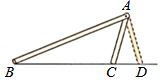 如图,△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等,这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.
如图,△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等,这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.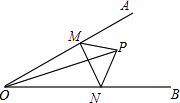 如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=8.
如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=8.