题目内容
（2012•宁德）如图，在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，EF∥AC∥HG，EH∥BD∥FG，则四边形EFGH的周长是（ ）分析：根据矩形的对角线相等，利用勾股定理求出对角线的长度，然后根据平行线分线段成比例定理列式表示出EF、EH的长度之和，再根据四边形EFGH是平行四边形，即可得解．
解答：解：在矩形ABCD中，AB=2，BC=3，
根据勾股定理，AC=BD=
=
=
，
∵EF∥AC∥HG，
∴
=
，
∵EH∥BD∥FG，
∴
=
，
∴
+
=
+
=1，
∴EF+EH=AC=
，
∵EF∥HG，EH∥FG，
∴四边形EFGH是平行四边形，
∴四边形EFGH的周长=2（EF+EH）=2
．
故选D．
根据勾股定理，AC=BD=
| AB2+BC2 |
| 22+32 |
| 13 |
∵EF∥AC∥HG，
∴
| EF |
| AC |
| EB |
| AB |
∵EH∥BD∥FG，
∴
| EH |
| BD |
| AE |
| AB |
∴
| EF |
| AC |
| EH |
| BD |
| EB |
| AB |
| AE |
| AB |
∴EF+EH=AC=
| 13 |
∵EF∥HG，EH∥FG，
∴四边形EFGH是平行四边形，
∴四边形EFGH的周长=2（EF+EH）=2
| 13 |
故选D．
点评：本题考查了平行线分线段成比例定理，矩形的对角线相等，勾股定理，根据平行线分线段成比例定理求出
+
=1是解题的关键，也是本题的难点．
| EF |
| AC |
| EH |
| BD |
练习册系列答案
相关题目
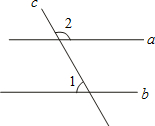（2012•宁德）如图，直线a∥b，∠1=60°，则∠2=
（2012•宁德）如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，∠D=30°．
（2012•宁德）如图，在菱形ABCD中，点E、F分别是BD、CD的中点，EF=6cm，则AB=