题目内容

（2012•宁德）如图，在菱形ABCD中，点E、F分别是BD、CD的中点，EF=6cm，则AB=
12
12
cm．
分析：连接AC，得出∠DEC=90°，根据直角三角形斜边上中线性质得出EF=
1
2
CD，求出CD即可．
解答：解：
连接AC，
∵四边形ABCD是菱形，
∴AB=CD，AC⊥BD，
∴∠DEC=90°，
∵F为CD的中点，
∴EF=
1
2
CD=6，
∴CD=12，
∴AB=CD=12，
故答案为：12．
点评：本题考查了直角三角形斜边上中线，三角形的中位线，菱形的性质，关键是求出EF=
1
2
CD．
练习册系列答案
相关题目
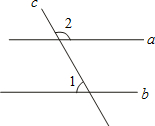（2012•宁德）如图，直线a∥b，∠1=60°，则∠2=
120
120
°．
（2012•宁德）如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴的负半轴上，且OD=10，OB=8，将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合
（1）直接写出点A、B的坐标：A（
6
6
，
0
0
）、B（
0
0
，
-8
-8
）；
（2）若抛物线y=-
1
3
x2+bx+c经过A、B两点，则这条抛物线的解析式是
y=-
1
3
x2+
10
3
x-8
y=-
1
3
x2+
10
3
x-8
；
（3）若点M是直线AB上方抛物线上的一个动点，作MN⊥x轴于点N，问是否存在点M，使△AMN与△ACD相似？若存在，求出点M的横坐标；若不存在，说明理由；
（4）当
7
2
≤x≤7时，在抛物线上存在点P，使△ABP得面积最大，求△ABP面积的最大值．
（2012•宁德）如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，∠D=30°．
（1）求∠A的度数；
（2）过点C作CF⊥AB，垂足为E，交⊙O于点F，CF=4
3
，求弧BC的长度．（结果保留π）
（2012•宁德）如图，在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，EF∥AC∥HG，EH∥BD∥FG，则四边形EFGH的周长是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网