Question

如图，在等腰梯形ABCD中，AD∥BC，对角线AC、BD把等腰梯形分成了四个小三角形，任意选取其中两个小三角形是全等三角形的概率是________．

Answer 1

分析：首先根据等腰梯形的性质，可证得②与④全等，又由树状图，可得所有等可能的结果与任意选取其中两个小三角形是全等三角形的情况，然后有概率公式即可求得答案．
解答：解：∵AD∥BC，
∴△AOD∽△COB，
∵AB=AC，
∴∠ABC=∠DCB，
∵AB=CD，BC=CB，
∴△ABC≌△DCB，
∴∠ACB=∠DBC，
∵∠AOB=∠DOC，
∴△AOB≌△DOC．
画树状图得：
∴一共有12种等可能的结果，
任意选取其中两个小三角形是全等三角形的有2种，
∴任意选取其中两个小三角形是全等三角形的概率是=．
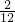故答案为：．
点评：此题考查了等腰梯形的性质，全等三角形的判定，以及树状图法求概率．此题综合性较强，难度适中，用到的知识点为：概率=所求情况数与总情况数之比．